The solution to the problem of the discontinuity of histograms can be effectively addressed with a simple method. Given a sample xi ∈ X, it's possible to consider a hypervolume (normally a hypercube or a hypersphere), assuming that we are working with multivariate distributions, whose center is xi. The extension of such a region is defined through a constant h called bandwidth (the name has been chosen to support the meaning of a limited area where the value is positive). However, instead of simply counting the number of samples belonging to the hypervolume, we now approximate this value using a smooth kernel function K(xi; h) with some important features:
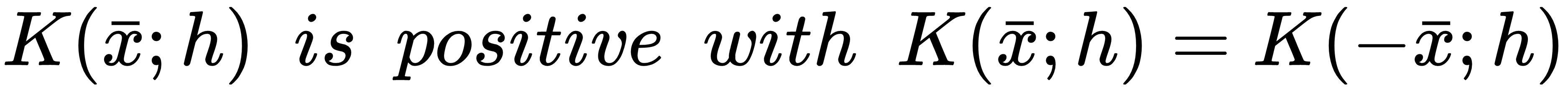
Moreover, for statistical and practical reasons, it's also necessary to enforce the following integral constraints (for simplicity, they are shown only for a univariate case...











































































