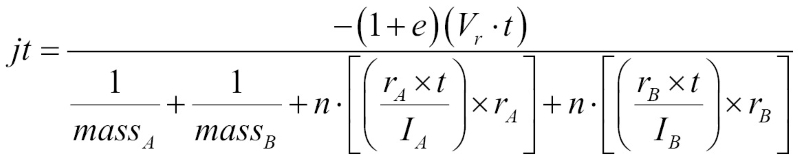Angular Impulse
Now that we have orientation, collisions require both a linear and angular response. This means we need an equation that gives us the impulse magnitude in terms of both linear and angular components.
From the previous section, Linear Impulse, we already know the linear impulse of the collision:
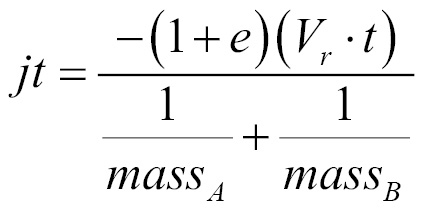
We need to find the angular component of this impulse. In the last section, Angular Velocity, we covered that the velocity of a point, P, at R distance away from the center of mass is given by the following equation:
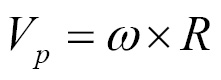
We can find the total velocity (linear plus angular) by adding the rotational velocity to the Linear Velocity of the rigidbody at the center of mass. We also need to find the torque from the point of impact and collision normal divided by the inertia tensor. Knowing this, we can find the final equation for j:
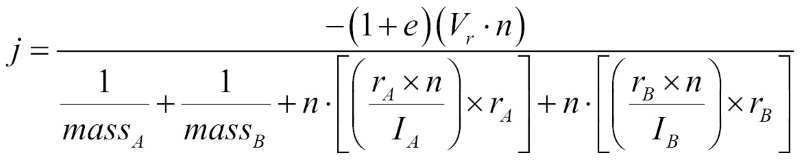
We must also update the formula for tangential impulse to apply friction. To do so, we replace all instances of the collision normal n with the tangent vector t: