Normalizing
A vector with a magnitude of 1 is a normal vector, sometimes called a unit vector. Whenever a vector has a length of 1, we can say that it has unit length. A normal vector is written as the letter of the vector with a caret symbol on top instead of an arrow,  . We can normalize any vector by dividing each of its components by the length of the vector:
. We can normalize any vector by dividing each of its components by the length of the vector:
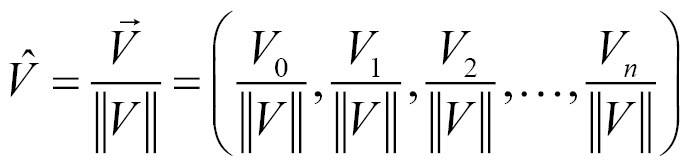
We never implemented division operators for the vector class. We can rewrite the preceding equation as reciprocal multiplication. This means we can obtain the normal of a vector if we multiply that vector by the inverse of its length:
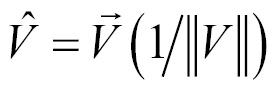
Getting ready
We are going to implement two functions, Normalize and Normalized. The first function will change the input vector to have a length of 1. The second function will not change the input vector; rather it will return a new vector with a length of 1.
How to do it…
Follow these steps to implement functions which will make a vector unit length or return a unit length vector. These steps utilize reciprocal multiplication.
- Declare the
NormalizeandNormalizedfunctions invectors.h:void Normalize(vec2& v); void Normalize(vec3& v); vec2 Normalized(const vec2& v); vec3 Normalized(const vec3& v);
- Add the implementation of these functions to
vectors.cpp:void Normalize(vec2& v) { v = v * (1.0f / Magnitude(v)); } void Normalize(vec3& v) { v = v * (1.0f / Magnitude(v)); } vec2 Normalized(const vec2& v) { return v * (1.0f / Magnitude(v)); } vec3 Normalized(const vec3& v) { return v * (1.0f / Magnitude(v)); }
How it works…
Normalizing works by scaling the vector by the inverse of its length. This scale makes the vector have unit length, which is a length of 1. Unit vectors are special as any number multiplied by 1 stays the same number. This makes unit vectors ideal for representing a direction. If a direction has unit length, scaling it by some velocity becomes trivial.




























































