Understanding the dynamics of point particles
The trajectory of a point particle over time t is calculated from its mass m and net force
of a point particle over time t is calculated from its mass m and net force  using Newton's equation, as illustrated here:
using Newton's equation, as illustrated here:
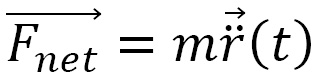
 is determined from the sum of all forces acting on the particle. In a system of interacting particles, the force
is determined from the sum of all forces acting on the particle. In a system of interacting particles, the force  acting between one pair of particles can be determined from the gradient of the potential energy function
acting between one pair of particles can be determined from the gradient of the potential energy function  . Here,
. Here,  is the displacement vector that points to the particle for which we are calculating
is the displacement vector that points to the particle for which we are calculating  (using the following equation) and originates from the other particle in the pair (shown in Figure 1.1):
(using the following equation) and originates from the other particle in the pair (shown in Figure 1.1):
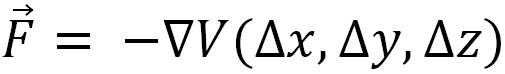
This gives us the three components of  . The (x) force component is given as follows:
. The (x) force component is given as follows:
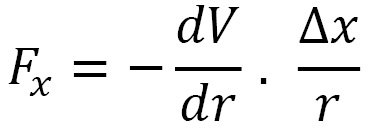
The (y) force component is calculated by the following formula:
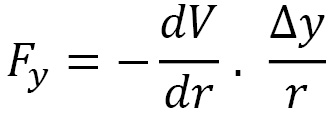
The (z) force component is given by the following formula:
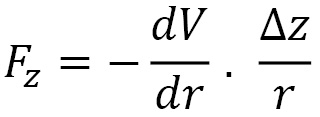
Here,  is the distance between the pair of particles. By Newton's third law, it follows that the force components acting on the other particle in the pair have the same magnitudes, with the opposite sign.
is the distance between the pair of particles. By Newton's third law, it follows that the force components acting on the other particle in the pair have the same magnitudes, with the opposite sign.
The following diagram illustrates this concept, using two particles interacting via a 12-6 Lennard-Jones potential of the form  , where
, where  represents the well depth and
represents the well depth and  represents the position at which the potential is zero:
represents the position at which the potential is zero:
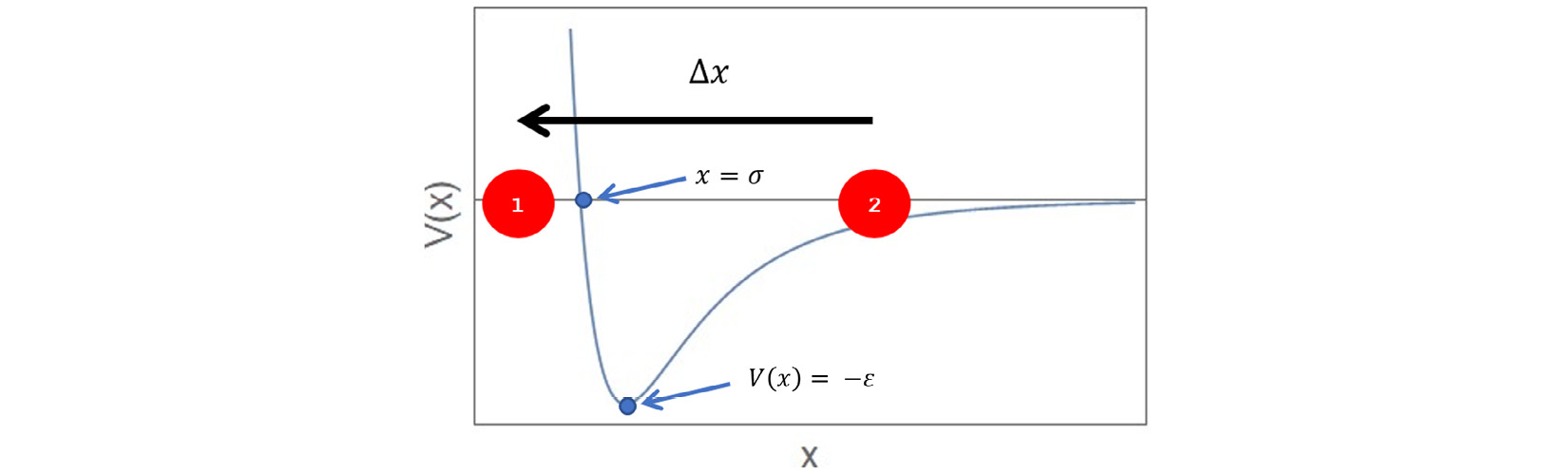
Figure 1.1 – Two particles in 1D interact via a Lennard-Jones potential 
In this diagram, if we want to calculate the force from particle 2 (located at  ) acting on particle 1 (located at
) acting on particle 1 (located at  ), then we use
), then we use  . Subsequently, the reaction force acting on particle 2 is given by
. Subsequently, the reaction force acting on particle 2 is given by  .
.
Since potential energy functions are commonly expressed as functions of r, the expressions we saw earlier make it more convenient to calculate the force components. The sum of forces acting on a single particle by its interaction with all particles in the system gives the net force, as illustrated here:
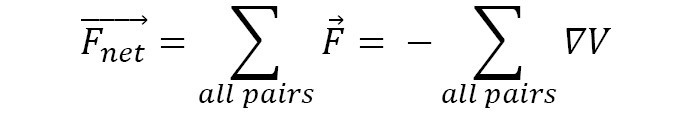
Altogether, we obtain three equations to solve for  , and
, and  . The x(t) equation is given as follows:
. The x(t) equation is given as follows:
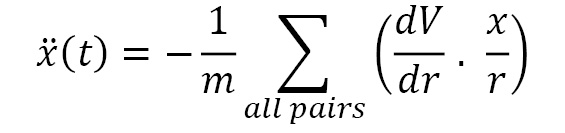
The y(t) equation is given by the following formula:
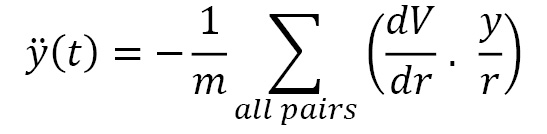
The z(t) equation is given by the following formula:
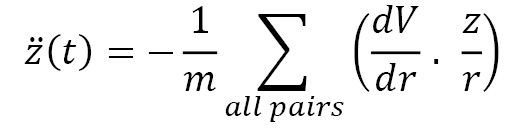
These values are used to generate the complete trajectory of the particle over a desired time interval. This process is repeated for all particles in the system to yield the complete system time evolution in the same time interval.
































































