Pearson's correlation

Pearson's correlation is often given the variable name r and is calculated in the following way, where dx_i and dy_i are calculated as before:

Since the standard deviations are constant values for the variables X and Y the equation can be simplified to the following, where σ_x and σ_y are the standard deviations of X and Y respectively:

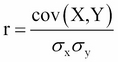
This is sometimes referred to as Pearson's product-moment correlation coefficient or simply just the correlation coefficient and is usually denoted by the letter r.

We have previously written functions to calculate the standard deviation. Combining with our function to calculate covariance yields the following implementation of Pearson's correlation:

(defn correlation [x y]
  (/ (covariance x y)
     (* (standard-deviation x)
        (standard-deviation y))))

Alternately, we can make use of the incanter.stats/correlation function.

Because standard scores are dimensionless, so is r. If r is -1.0 or 1.0, the variables are perfectly negatively or...