Differential and integral calculus
In this section, we won’t go into the fundamentals of differential calculus, but instead just recap some basic results and notation. Therefore, we are assuming you already have some basic familiarity with differentiation and integration.
Differentiation
Let’s start with what the derivative of a function or curve 
intuitively represents. An example curve is shown in Figure 1.5. The derivative of this function is denoted by the following symbol:
Eq. 29
The derivative of 
is itself a function of 
. The numerical value of the derivative evaluated at a particular value of 
, let’s say at 
, is the gradient (or slope) of the tangent to the curve 
at 
. As such, we can think of the derivative as defining the local gradient value of the curve. This is illustrated in Figure 1.5 as well:
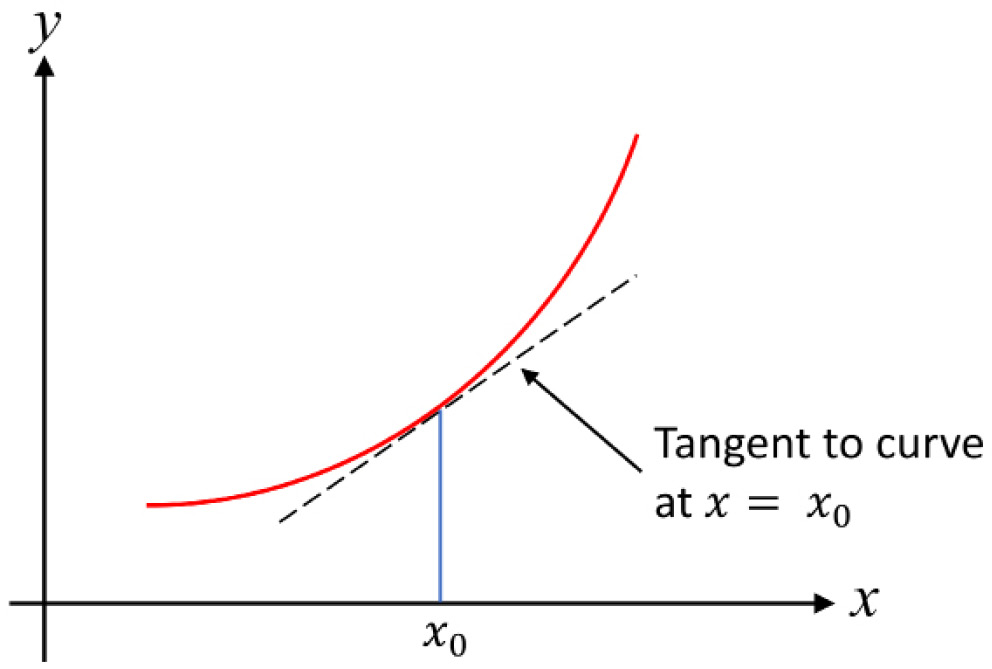
Figure 1.5: The derivative as the gradient of the tangent to the curve
Sometimes, when we want to be explicit...
