You're reading from The Deep Learning Workshop Learn the skills you need to develop your own next-generation deep learning models with TensorFlow and Keras

Product type Paperback

Published in Jul 2020

Publisher Packt

ISBN-13 9781839219856

Length 474 pages

Edition 1st Edition

Languages

Python

Tools

Keras

Concepts

Deep Learning

Authors (5):

Nipun Sadvilkar

Thomas Joseph

Anthony So

Mohan Kumar Silaparasetty

Mirza Rahim Baig

+1 more

View More author details

Table of Contents (9) Chapters

Preface

1. Building Blocks of Deep Learning

2. Neural Networks FREE CHAPTER

3. Image Classification with Convolutional Neural Networks (CNNs)

4. Deep Learning for Text – Embeddings

5. Deep Learning for Sequences

6. LSTMs, GRUs, and Advanced RNNs

7. Generative Adversarial Networks

Appendix

Introduction to TensorFlow

TensorFlow is a deep learning library developed by Google. At the time of writing this book, TensorFlow is by far the most popular deep learning library. It was originally developed by a team within Google called the Google Brain team for their internal use and was subsequently open sourced in 2015. The Google Brain team has developed popular applications such as Google Photos and Google Cloud Speech-to-Text, which are deep learning applications based on TensorFlow. TensorFlow 1.0 was released in 2017, and within a short period of time, it became the most popular deep learning library ahead of other existing libraries, such as Caffe, Theano, and PyTorch. It is considered the industry standard, and almost every organization that is doing something in the deep learning space has adopted it. Some of the key features of TensorFlow are as follows:

It can be used with all common programming languages, such as Python, Java, and R
It can be deployed on multiple platforms, including Android and Raspberry Pi
It can run in a highly distributed mode and hence is highly scalable

After being in Alpha/Beta release for a long time, the final version of TensorFlow 2.0 was released on September 30, 2019. The focus of TF2.0 was to make the development of deep learning applications easier. Let's go ahead and understand the basics of the TensorFlow 2.0 framework.

Tensors

Inside the TensorFlow program, every data element is called a tensor. A tensor is a representation of vectors and matrices in higher dimensions. The rank of a tensor denotes its dimensions. Some of the common data forms represented as tensors are as follows.

Scalar

A scalar is a tensor of rank 0, which only has magnitude.

For example, [ 12 ] is a scalar of magnitude 12.

Vector

A vector is a tensor of rank 1.

For example, [ 10 , 11, 12, 13].

Matrix

A matrix is a tensor of rank 2.

For example, [ [10,11] , [12,13] ]. This tensor has two rows and two columns.

Tensor of rank 3

This is a tensor in three dimensions. For example, image data is predominantly a three-dimensional tensor with width, height, and the number of channels as its three dimensions. The following is an example of a tensor with three dimensions, that is, it has two rows, three columns, and three channels:

Figure 1.10: Tensor with three dimensions

The shape of a tensor is represented by an array and indicates the number of elements in each dimension. For example, if the shape of a tensor is [2,3,5], it means the tensor has three dimensions. If this were to be image data, this shape would mean that this tensor has two rows, three columns, and five channels. We can also get the rank from the shape. In this example, the rank of the tensor is three, since there are three dimensions. This is further illustrated in the following diagram:

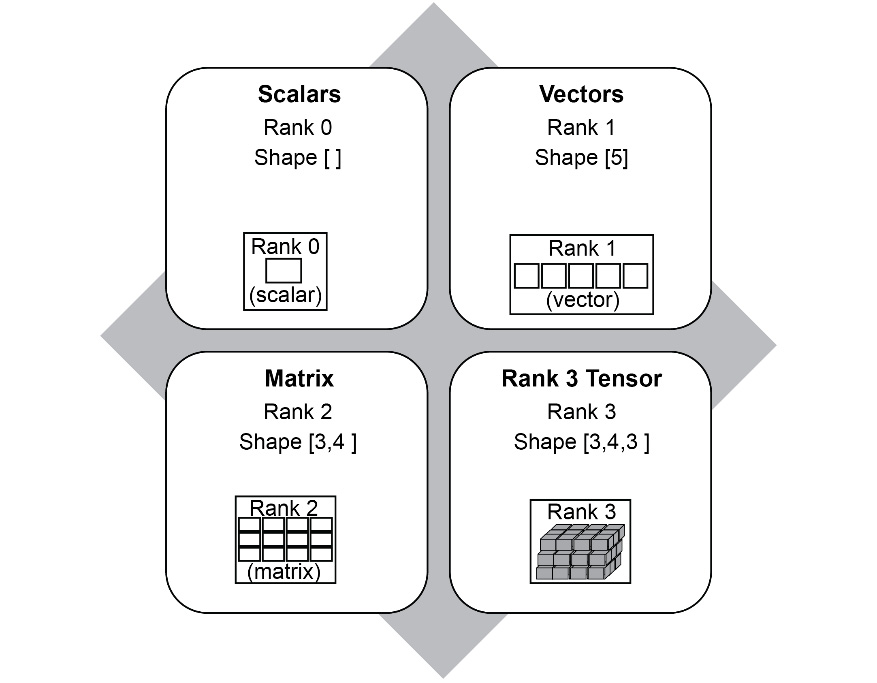
Figure 1.11: Examples of Tensor rank and shape

Constants

Constants are used to store values that are not changed or modified during the course of the program. There are multiple ways in which a constant can be created, but the simplest way is as follows:

a = tf.constant (10)

This creates a tensor initialized to 10. Keep in mind that a constant's value cannot be updated or modified by reassigning a new value to it. Another example is as follows:

s = tf.constant("Hello")

In this line, we are instantiating a string as a constant.

Variables

A variable is used to store data that can be updated and modified during the course of the program. We will look at this in more detail in Chapter 2, Neural Networks. There are multiple ways of creating a variable, but the simplest way is as follows:

b=tf.Variable(20)

In the preceding code, the variable b is initialized to 20. Note that in TensorFlow, unlike constants, the term Variable is written with an uppercase V.

A variable can be reassigned a different value during the course of the program. Variables can be used to assign any type of object, including scalars, vectors, and multi-dimensional arrays. The following is an example of how an array whose dimensions are 3 x 3 can be created in TensorFlow:

C = tf.Variable([[1,2,3],[4,5,6],[7,8,9]])

This variable can be initialized to a 3 x 3 matrix, as follows:

Figure 1.12: 3 x 3 matrix

Now that we know some of the basic concepts of TensorFlow, let's learn how to put them into practice.

Defining Functions in TensorFlow

A function can be created in Python using the following syntax:

def myfunc(x,y,c):
    Z=x*x*y+y+c
    return Z

A function is initiated using the special operator def, followed by the name of the function, myfunc, and the arguments for the function. In the preceding example, the body of the function is in the second line, and the last line returns the output.

In the following exercise, we will learn how to implement a small function using the variables and constants we defined earlier.

Exercise 1.02: Implementing a Mathematical Equation

In this exercise, we will solve the following mathematical equation using TensorFlow:

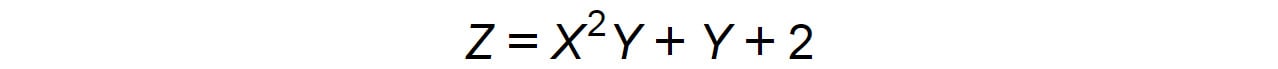
Figure 1.13: Mathematical equation to be solved using TensorFlow

We will use TensorFlow to solve it, as follows:

X=3
Y=4

While there are multiple ways of doing this, we will only explore one of the ways in this exercise. Follow these steps to complete this exercise:

Open a new Jupyter Notebook and rename it Exercise 1.02.
Import the TensorFlow library using the following command:
```
import tensorflow as tf
```
Now, let's solve the equation. For that, you will need to create two variables, X and Y, and initialize them to the given values of 3 and 4, respectively:
```
X=tf.Variable(3)
Y=tf.Variable(4)
```
In our equation, the value of 2 isn't changing, so we'll store it as a constant by typing the following code:
```
C=tf.constant(2)
```

Define the function that will solve our equation:

def myfunc(x,y,c):
    Z=x*x*y+y+c
    return Z

Call the function by passing X, Y, and C as parameters. We'll be storing the output of this function in a variable called result:
```
result=myfunc(X,Y,C)
```
Print the result using the tf.print() function:
```
tf.print(result)
```
The output will be as follows:
```
42
```
Note
To access the source code for this specific section, please refer to https://packt.live/2ClXKjj.
You can also run this example online at https://packt.live/2ZOIN1C. You must execute the entire Notebook in order to get the desired result.

In this exercise, we learned how to define and use a function. Those familiar with Python programming will notice that it is not a lot different from normal Python code.

In the rest of this chapter, we will prepare ourselves by looking at some basic linear algebra and familiarize ourselves with some of the common vector operations, so that understanding neural networks in the next chapter will be much easier.

Linear Algebra with TensorFlow

The most important linear algebra topic that will be used in neural networks is matrix multiplication. In this section, we will explain how matrix multiplication works and then use TensorFlow's built-in functions to solve some matrix multiplication examples. This is essential in preparation for neural networks in the next chapter.

How does matrix multiplication work? You might have studied this as part of high school, but let's do a quick recap.

Let's say we have to perform a matrix multiplication between two matrices, A and B, where we have the following:

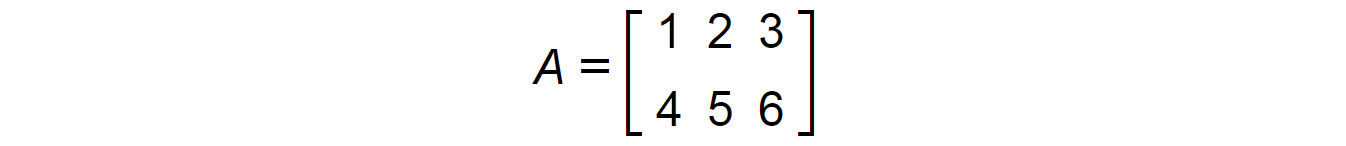
Figure 1.14: Matrix A

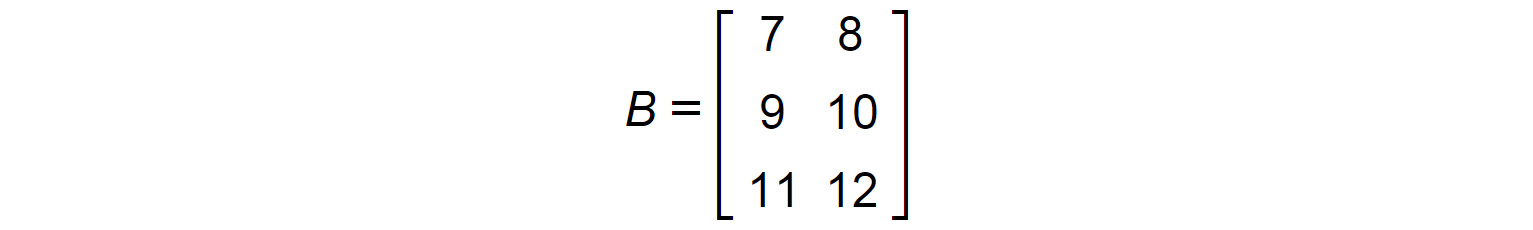
Figure 1.15: Matrix B

The first step would be to check whether multiplying a 2 x 3 matrix by a 3 x 2 matrix is possible. There is a prerequisite for matrix multiplication. Remember that C=R, that is, the number of columns (C) in the first matrix should be equal to the number of rows (R) in the second matrix. And remember the sequence matters here, and that's why, A x B is not equal to B x A. In this example, C=3 and R=3. So, multiplication is possible.

The resultant matrix would have the number of rows equal to that in A and the number of columns equal to that in B. So, in this case, the result would be a 2 x 2 matrix.

To begin multiplying the two matrices, take the elements of the first row of A (R1) and the elements of the first column of B (C1):

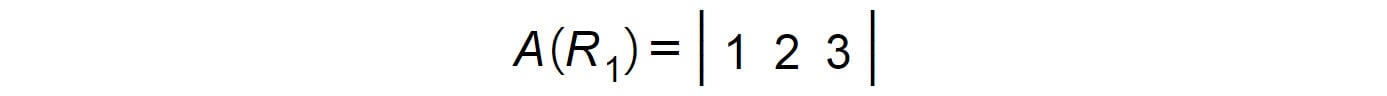
Figure 1.16: Matrix A(R1)

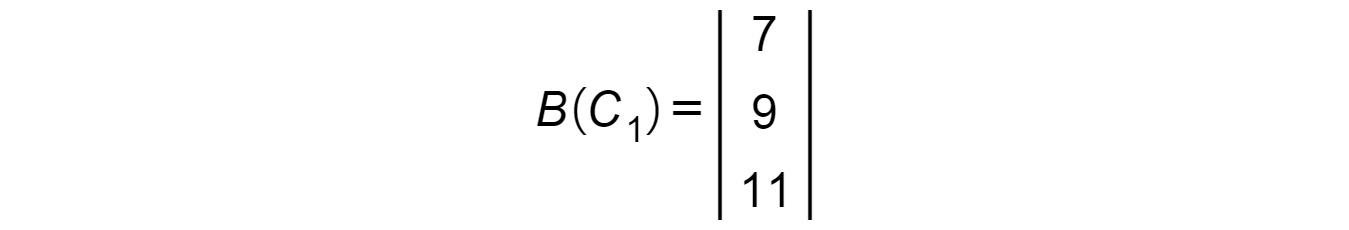
Figure 1.17: Matrix B(C1)

Get the sum of the element-wise products, that is, (1 x 7) + (2 x 9) + (3 x 11) = 58. This will be the first element in the resultant 2 x 2 matrix. We'll call this incomplete matrix D(i) for now:

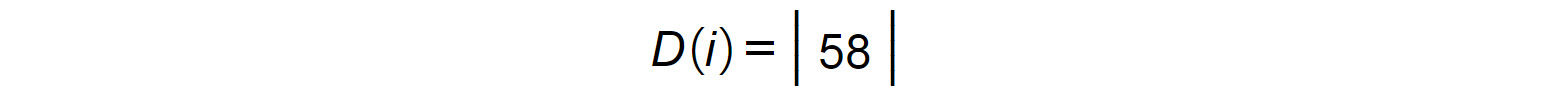
Figure 1.18: Incomplete matrix D(i)

Repeat this with the first row of A(R1) and the second column of B (C2):

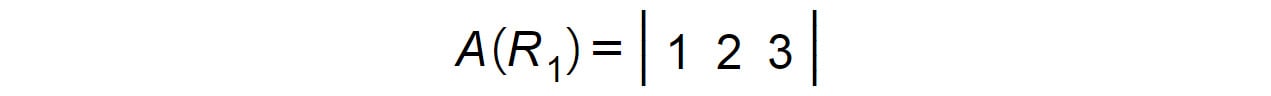
Figure 1.19: First row of matrix A

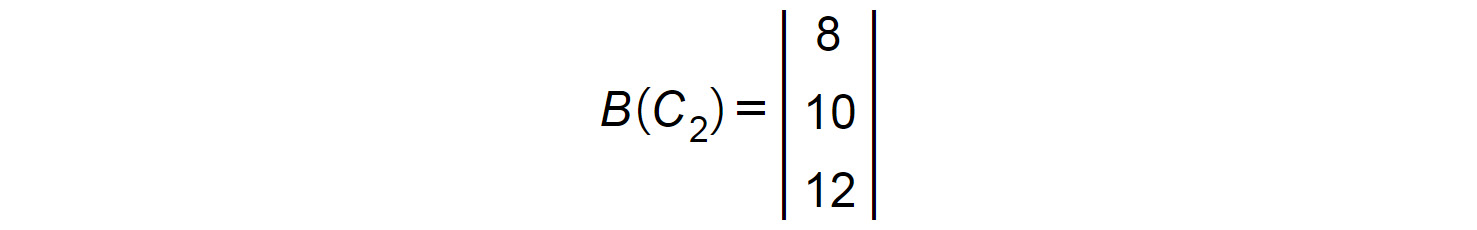
Figure 1.20: Second column of matrix B

Get the sum of the products of the corresponding elements, that is, (1 x 8) + (2 x 10) + (3 x 12) = 64. This will be the second element in the resultant matrix:

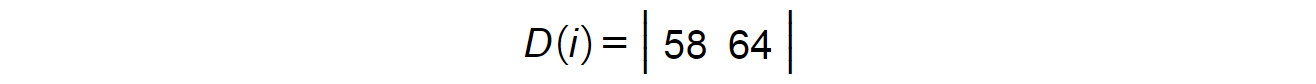
Figure 1.21: Second element of matrix D(i)

Repeat the same with the second row to get the final result:

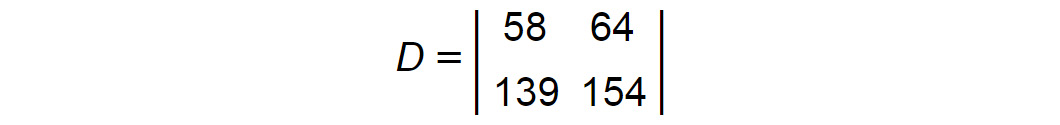
Figure 1.22: Matrix D

The same matrix multiplication can be performed in TensorFlow using a built-in method called tf.matmul(). The matrices that need to be multiplied must be supplied to the model as variables, as shown in the following example:

C = tf.matmul(A,B)

In the preceding case, A and B are the matrices that we want to multiply. Let's practice this method by using TensorFlow to multiply the two matrices we multiplied manually.

Exercise 1.03: Matrix Multiplication Using TensorFlow

In this exercise, we will use the tf.matmul() method to multiply two matrices using tensorflow. Follow these steps to complete this exercise:

Open a new Jupyter Notebook and rename it Exercise 1.03.
Import the tensorflow library and create two variables, X and Y, as matrices. X is a 2 x 3 matrix and Y is a 3 x 2 matrix:
```
import tensorflow as tf
X=tf.Variable([[1,2,3],[4,5,6]])
Y=tf.Variable([[7,8],[9,10],[11,12]])
```
Print and display the values of X and Y to make sure the matrices are created correctly. We'll start by printing the value of X:
```
tf.print(X)
```
The output will be as follows:
```
[[1 2 3]
 [4 5 6]]
```
Now, let's print the value of Y:
```
tf.print(Y)
```
The output will be as follows:
```
[[7 8]
 [9 10]
 [11 12]]
```
Perform matrix multiplication by calling the TensorFlow tf.matmul() function:
```
c1=tf.matmul(X,Y)
```
To display the result, print the value of c1:
```
tf.print(c1)
```
The output will be as follows:
```
[[58 64]
 [139 154]]
```
Let's perform matrix multiplication by changing the order of the matrices:
```
c2=tf.matmul(Y,X)
```
To display the result, let's print the value of c2:
```
tf.print(c2)
```
The resulting output will be as follows.
```
[[39 54 69]
 [49 68 87]
 [59 82 105]]
```
Note that the results are different since we changed the order.
Note
To access the source code for this specific section, please refer to https://packt.live/3eevyw4.
You can also run this example online at https://packt.live/2CfGGvE. You must execute the entire Notebook in order to get the desired result.

In this exercise, we learned how to create matrices in TensorFlow and how to perform matrix multiplication. This will come in handy when we create our own neural networks.

The reshape Function

Reshape, as the name suggests, changes the shape of a tensor from its current shape to a new shape. For example, you can reshape a 2 × 3 matrix to a 3 × 2 matrix, as shown here:

Figure 1.23: Reshaped matrix

Let's consider the following 2 × 3 matrix, which we defined as follows in the previous exercise:

X=tf.Variable([[1,2,3],[4,5,6]])

We can print the shape of the matrix using the following code:

X.shape

From the following output, we can see the shape, which we already know:

TensorShape([2, 3])

Now, to reshape X into a 3 × 2 matrix, TensorFlow provides a handy function called tf.reshape(). The function is implemented with the following arguments:

tf.reshape(X,[3,2])

In the preceding code, X is the matrix that needs to be reshaped, and [3,2] is the new shape that the X matrix has to be reshaped to.

Reshaping matrices is a handy operation when implementing neural networks. For example, a prerequisite when working with images using CNNs is that the image has to be of rank 3, that is, it has to have three dimensions: width, height, and depth. If our image is a grayscale image that has only two dimensions, the reshape operation will come in handy to add a third dimension. In this case, the third dimension will be 1:

Figure 1.24: Changing the dimension using reshape()

In the preceding figure, we are reshaping a matrix of shape [5,4] to a matrix of shape [5,4,1]. In the exercise that follows, we will be using the reshape() function to reshape a [5,4] matrix.

There are some important considerations when implementing the reshape() function:

The total number of elements in the new shape should be equal to the total number of elements in the original shape. For example, you can reshape a 2 × 3 matrix (a total of 6 elements) to a 3 × 2 matrix since the new shape also has 6 elements. However, you cannot reshape it to 3 × 3 or 3 × 4.
The reshape() function should not be confused with transpose(). In reshape(), the sequence of the elements of the matrix is retained and the elements are rearranged in the new shape in the same sequence. However, in the case of transpose(), the rows become columns and the columns become rows. Hence the sequence of the elements will change.
The reshape() function will not change the original matrix unless you assign the new shape to it. Otherwise, it simply displays the new shape without actually changing the original variable. For example, let's say x has shape [2,3] and you simply run tf.reshape(x,[3,2]). When you check the shape of x again, it will remain as [2,3]. In order to actually change the shape, you need to assign the new shape to it, like this:
```
x=tf.reshape(x,[3,2])
```

Let's try implementing reshape() in TensorFlow in the exercise that follows.

Exercise 1.04: Reshaping Matrices Using the reshape() Function in TensorFlow

In this exercise, we will reshape a [5,4] matrix into the shape of [5,4,1] using the reshape() function. This exercise will help us understand how reshape() can be used to change the rank of a tensor. Follow these steps to complete this exercise:

Open a Jupyter Notebook and rename it Exercise 1.04. Then, import tensorflow and create the matrix we want to reshape:

import tensorflow as tf
A=tf.Variable([[1,2,3,4], \
               [5,6,7,8], \
               [9,10,11,12], \
               [13,14,15,16], \
               [17,18,19,20]])

First, we'll print the variable A to check whether it is created correctly, using the following command:
```
tf.print(A)
```
The output will be as follows:
```
[[1 2 3 4]
 [5 6 7 8]
 [9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]]
```
Let's print the shape of A, just to be sure:
```
A.shape
```
The output will be as follows:
```
TensorShape([5, 4])
```
Currently, it has a rank of 2. We'll be using the reshape() function to change its rank to 3.

Now, we will reshape A to the shape [5,4,1] using the following command. We've thrown in the print command just to see what the output looks like:

tf.print(tf.reshape(A,[5,4,1]))

We'll get the following output:

[[[1]
  [2]
  [3]
  [4]]
 [[5]
  [6]
  [7]
  [8]]
 [[9]
  [10]
  [11]
  [12]]
 [[13]
  [14]
  [15]
  [16]]
 [[17]
  [18]
  [19]
  [20]]]

That worked as expected.

Let's see the new shape of A:
```
A.shape
```
The output will be as follows:
```
TensorShape([5, 4])
```
We can see that A still has the same shape. Remember that we discussed that in order to save the new shape, we need to assign it to itself. Let's do that in the next step.
Here, we'll assign the new shape to A:
```
A = tf.reshape(A,[5,4,1])
```
Let's check the new shape of A once again:
```
A.shape
```
We will see the following output:
```
TensorShape([5, 4, 1])
```
With that, we have not just reshaped the matrix but also changed its rank from 2 to 3. In the next step, let's print out the contents of A just to be sure.
Let's see what A contains now:
```
tf.print(A)
```
The output, as expected, will be as follows:
```
[[[1]
  [2]
  [3]
  [4]]
 [[5]
  [6]
  [7]
  [8]]
 [[9]
  [10]
  [11]
  [12]]
 [[13]
  [14]
  [15]
  [16]]
 [[17]
  [18]
  [19]
  [20]]]
```
Note
To access the source code for this specific section, please refer to https://packt.live/3gHvyGQ.
You can also run this example online at https://packt.live/2ZdjdUY. You must execute the entire Notebook in order to get the desired result.

In this exercise, we saw how to use the reshape() function. Using reshape(), we can change the rank and shape of tensors. We also learned that reshaping a matrix changes the shape of the matrix without changing the order of the elements within the matrix. Another important thing that we learned was that the reshape dimension has to align with the number of elements in the matrix. Having learned about the reshape function, we will go ahead and learn about the next function, which is Argmax.

The argmax Function

Now, let's understand the argmax function, which is frequently used in neural networks. Argmax returns the position of the maximum value along a particular axis in a matrix or tensor. It must be noted that it does not return the maximum value, but rather the index position of the maximum value.

For example, if x = [1,10,3,5], then tf.argmax(x) will return 1 since the maximum value (which in this case is 10) is in the index position 1.

Note

In Python, the index starts with 0. So, considering the preceding example of x, the element 1 will have an index of 0, 10 will have an index of 1, and so on.

Now, let's say we have the following:

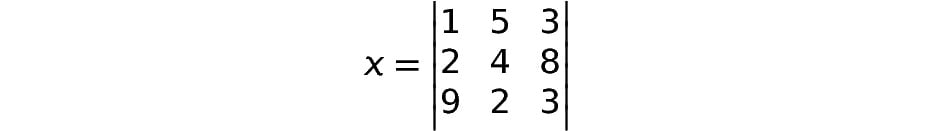
Figure 1.25: An example matrix

In this case, argmax has to be used with the axis parameter. When axis equals 0, it returns the position of the maximum value in each column, as shown in the following figure:

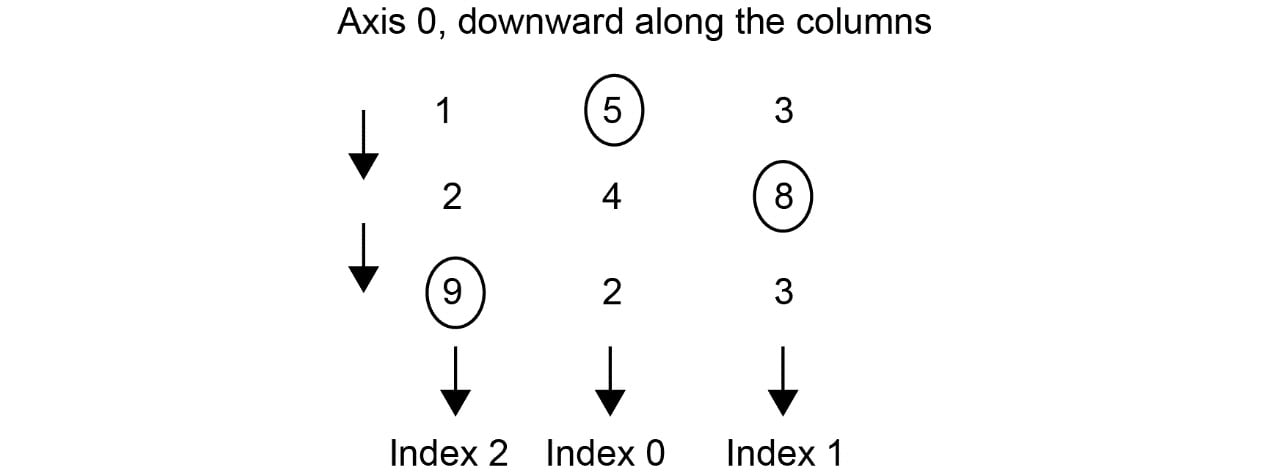
Figure 1.26: The argmax operation along axis 0

As you can see, the maximum value in the first column is 9, so the index, in this case, will be 2. Similarly, if we move along to the second column, the maximum value is 5, which has an index of 0. In the third column, the maximum value is 8, and hence the index is 1. If we were to run the argmax function on the preceding matrix with the axis as 0, we would get the following output:

[2,0,1]

When axis = 1, argmax returns the position of the maximum value across each row, like this:

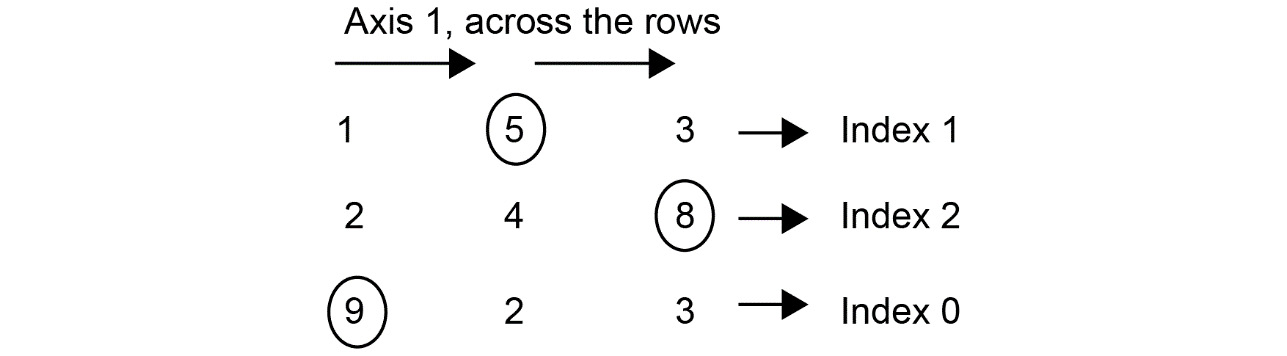
Figure 1.27: The argmax operation along axis 1

Moving along the rows, we have 5 at index 1, 8 at index 2, and 9 at index 0. If we were to run the argmax function on the preceding matrix with the axis as 1, we would get the following output:

[1,2,0]

With that, let's try and implement argmax on a matrix.

Exercise 1.05: Implementing the argmax() Function

In this exercise, we are going to use the argmax function to find the position of the maximum value in a given matrix along axes 0 and 1. Follow these steps to complete this exercise:

Import tensorflow and create the following matrix:

import tensorflow as tf
X=tf.Variable([[91,12,15], [11,88,21],[90, 87,75]])

Let's print X and see what the matrix looks like:
```
tf.print(X)
```
The output will be as follows:
```
[[91 12 15]
 [11 88 21]
 [90 87 75]]
```
Print the shape of X:
```
X.shape
```
The output will be as follows:
```
TensorShape([3, 3])
```
Now, let's use argmax to find the positions of the maximum values while keeping axis as 0:
```
tf.print(tf.argmax(X,axis=0))
```
The output will be as follows:
```
[0 1 2]
```
Referring to the matrix in Step 2, we can see that, moving across the columns, the index of the maximum value (91) in the first column is 0. Similarly, the index of the maximum value along the second column (88) is 1. And finally, the maximum value across the third column (75) has index 2. Hence, we have the aforementioned output.
Now, let's change the axis to 1:
```
tf.print(tf.argmax(X,axis=1))
```
The output will be as follows:
```
[0 1 0]
```

Again, referring to the matrix in Step 2, if we move along the rows, the maximum value along the first row is 91, which is at index 0. Similarly, the maximum value along the second row is 88, which is at index 1. Finally, the third row is at index 0 again, with a maximum value of 75.

Note

To access the source code for this specific section, please refer to https://packt.live/2ZR5q5p.

You can also run this example online at https://packt.live/3eewhNO. You must execute the entire Notebook in order to get the desired result.

In this exercise, we learned how to use the argmax function to find the position of the maximum value along a given axis of a tensor. This will be used in the subsequent chapters when we perform classification using neural networks.

Optimizers

Before we look at neural networks, let's learn about one more important concept, and that is optimizers. Optimizers are extensively used for training neural networks, so it is important to understand their application. In this chapter, let's get a basic introduction to the concept of an optimizer. As you might already be aware, the purpose of machine learning is to find a function (along with its parameters) that maps inputs to outputs.

For example, let's say the original function of a data distribution is a linear function (linear regression) of the following form:

Y = mX + b

Here, Y is the dependent variable (label), X the independent variable (features), and m and b are the parameters of the model. Solving this problem with machine learning would entail learning the parameters m and b and thereby the form of the function that connects X to Y. Once the parameters have been learned, if we are given a new value for X, we can calculate or predict the value of Y. It is in learning these parameters that optimizers come into play. The learning process entails the following steps:

Assume some arbitrary random values for the parameters m and b.
With these assumed parameters, for a given dataset, estimate the values of Y for each X variable.
Find the difference between the predicted value of Y and the actual value of Y associated with the X variable. This difference is called the loss function or cost function. The magnitude of loss will depend on the parameter values we initially assumed. If the assumptions were way off the actual values, then the loss will be high. The way to get toward the right parameter is by changing or altering the initial assumed values of the parameters in such a way that the loss function is minimized. This task of changing the values of the parameters to reduce the loss function is called optimization.

There are different types of optimizers that are used in deep learning. Some of the most popular ones are stochastic gradient descent, Adam, and RMSprop. The detailed functionality and the internal workings of optimizers will be described in Chapter 2, Neural Networks, but here, we will see how they are applied in solving certain common problems, such as simple linear regression. In this chapter, we will be using an optimizer called Adam, which is a very popular optimizer. We can define the Adam optimizer in TensorFlow using the following code:

tf.optimizers.Adam()

Once an optimizer has been defined, we can use it to minimize the loss using the following code:

optimizer.minimize(loss,[m,b])

The terms [m,b] are the parameters that will be changed during the optimization process. Now, let's use an optimizer to train a simple linear regression model using TensorFlow.

Exercise 1.06: Using an Optimizer for a Simple Linear Regression

In this exercise, we are going to see how to use an optimizer to train a simple linear regression model. We will start off by assuming arbitrary values for the parameters (w and b) in a linear equation w*x + b. Using the optimizer, we will observe how the values of the parameters change to get to the right parameter values, thus mapping the relationship between the input values (x) and output (y). Using the optimized parameter values, we will predict the output (y) for some given input values (x). After completing this exercise, we will see that the linear output, which is predicted by the optimized parameters, is very close to the real values of the output values. Follow these steps to complete this exercise:

Open a Jupyter Notebook and rename it Exercise 1.06.
Import tensorflow, create the variables, and initialize them to 0. Here, our assumed values are zero for both these parameters:
```
import tensorflow as tf
w=tf.Variable(0.0)
b=tf.Variable(0.0)
```
Define a function for the linear regression model. We learned how to create functions in TensorFlow earlier:
```
def regression(x):
    model=w*x+b
    return model
```
Prepare the data in the form of features (x) and labels (y):
```
x=[1,2,3,4]
y=[0,-1,-2,-3]
```
Define the loss function. In this case, this is the absolute value of the difference between the predicted value and the label:
```
loss=lambda:abs(regression(x)-y)
```
Create an Adam optimizer instance with a learning rate of .01. The learning rate defines at what rate the optimizer should change the assumed parameters. We will discuss the learning rate in subsequent chapters:
```
optimizer=tf.optimizers.Adam(.01)
```
Train the model by running the optimizer for 1,000 iterations to minimize the loss:
```
for i in range(1000):
    optimizer.minimize(loss,[w,b])
```
Print the trained values of the w and b parameters:
```
tf.print(w,b)
```
The output will be as follows:
```
-1.00371706 0.999803364
```
We can see that the values of the w and b parameters have been changed from their original values of 0, which were assumed. This is what is done during the optimizing process. These updated parameter values will be used for predicting the values of Y.
Note
The optimization process is stochastic in nature (having a random probability distribution), and you might get values for w and b that are different to the value that was printed here.
Use the trained model to predict the output by passing in the x values. The model predicts the values, which are very close to the label values (y), which means the model was trained to a high level of accuracy:
```
tf.print(regression([1,2,3,4]))
```
The output of the preceding command will be as follows:
```
[-0.00391370058 -1.00763083 -2.01134801 -3.01506495]
```
Note
To access the source code for this specific section, please refer to https://packt.live/3gSBs8b.
You can also run this example online at https://packt.live/2OaFs7C. You must execute the entire Notebook in order to get the desired result.

In this exercise, we saw how to use an optimizer to train a simple linear regression model. During this exercise, we saw how the initially assumed values of the parameters were updated to get the true values. Using the true values of the parameters, we were able to get the predictions close to the actual values. Understanding how to apply the optimizer will help you later with training neural network models.

Now that we have seen the use of an optimizer, let's take what we've learned and apply the optimization function to solve a quadratic equation in the next activity.

Activity 1.01: Solving a Quadratic Equation Using an Optimizer

In this activity, you will use an optimizer to solve the following quadratic equation:

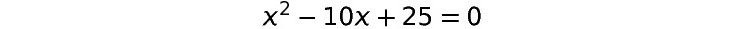
Figure 1.28: A quadratic equation

Here are the high-level steps you need to follow to complete this activity:

Open a new Jupyter Notebook and import the necessary packages, just as we did in the previous exercises.
Initialize the variable. Please note that, in this example, x is the variable that you will need to initialize. You can initialize it to a value of 0.
Construct the loss function using the lambda function. The loss function will be the quadratic equation that you are trying to solve.
Use the Adam optimizer with a learning rate of .01.
Run the optimizer for different iterations and minimize the loss. You can start the number of iterations at 1,000 and then increase it in subsequent trials until you get the result you desire.
Print the optimized value of x.