Rejection sampling
Suppose we want to sample from a distribution that is not a simple one. Let's call this distribution p(x) and let's assume we can evaluate p(x) for any given value x, up to a normalizing constant Z, that is:
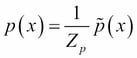
In this context, p(x) is too complex to sample from but we have another simpler distribution q(x) from which we can draw samples. Next, we assume there exists a constant k such that  for all values of x. The function kq(x) is the comparison function as shown in the following figure:
for all values of x. The function kq(x) is the comparison function as shown in the following figure:
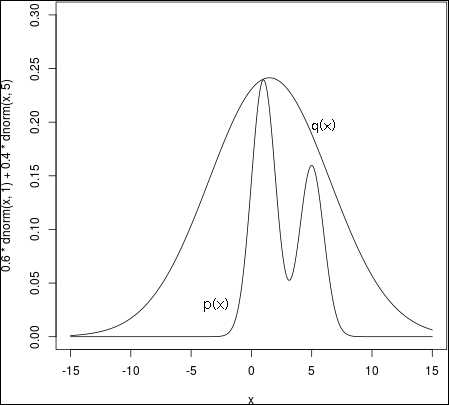
The distribution p(x) has been generated with a simple plot:
0.6*dnorm(x,1)+0.4*dnorm(x,5)
The rejection sampling algorithm is based on the following idea:
Draw a sample z0 from q(z), the proposal distribution
- Draw a second u0 sample from a uniform distribution on [0, kq(z0)]
-
If
 then the sample is rejected otherwise u0 is accepted
then the sample is rejected otherwise u0 is accepted
In the following figure, the pair (z0, u0) is rejected if it lies in the gray area. The accepted pairs are a uniform distribution under the curve of p(z) and therefore...






















































