Stochastic processes
A stochastic process is a family of random variables that depends on a parameter, t. A stochastic process is specified using the following notation:
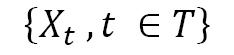
Here, t is a parameter, and T is the set of possible values of t.
Usually, time is indicated by t, so a stochastic process is a family of time-dependent random variables. The variability range of t, that is, the set, T, can be a set of real numbers, possibly coinciding with the entire time axis. But it can also be a discrete set of values.
The random variables, Xt, are defined on the set, X, called the space of states. This can be a continuous set, in which case it is defined as a continuous stochastic process, or a discrete set, in which case it is defined as a discrete stochastic process.
Consider the following elements:
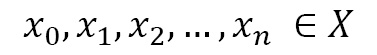
This means the values that the random variables, Xt, can take are called system states and represent the possible results of an experiment...




























































