Polynomial regression
The previous analysis has been centered around the idea of obtaining a linear equation to represent a given dataset. However, many datasets derive from non-linear relationships. Fortunately, there are alternative mathematical models from which to choose.
The simplest nonlinear functions are polynomials: y = f(x) b0 + b1x + b2x2 + …+bdxd, where d is the degree of the polynomial and b0, b1, b2, ..., bm are the coefficients to be determined.
Of course, a linear function is simply a first-degree polynomial: y = b0 + b1x. We have already solved that problem (in the previous derivation, we called the coefficients m and b instead of b1 and b0). We used the method of least squares to derive the formulas for the coefficients:
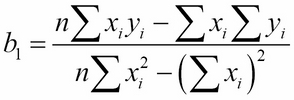
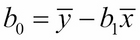
Those formulas were derived from the normal equations:
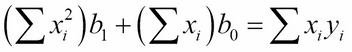
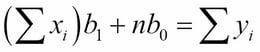
The equations were obtained by minimizing the sum of squares:
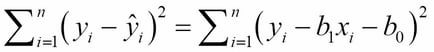
We can apply the same least squares method to find the best-fitting polynomial of any degree d for a given dataset, provided that d is less than...



































































