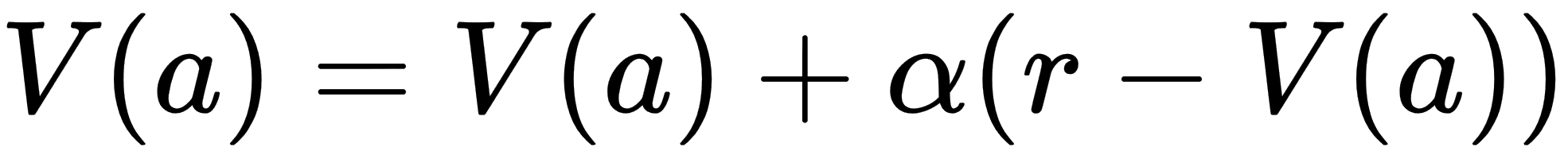Since this is our first example, make sure your Python environment is set to go. Again for simplicity, we prefer Anaconda. Make sure you are comfortable coding with your chosen IDE and open up the code example, Chapter_1_1.py, and follow along:
- Let's examine the first section of the code, as shown here:
import random
reward = [1.0, 0.5, 0.2, 0.5, 0.6, 0.1, -.5]
arms = len(reward)
episodes = 100
learning_rate = .1
Value = [0.0] * arms
print(Value)
- We first start by doing import of random. We will use random to randomly select an arm during each training episode.
- Next, we define a list of rewards, reward. This list defines the reward for each arm (action) and hence defines the number of arms/actions on the bandit.
- Then, we determine the number of arms using the len() function.
- After that, we set the number of training episodes our agent will use to evaluate the value of each arm.
- Set the learning_rate value to .1. This means the agent will learn slowly the value of each pull.
- Next, we initialize the value for each action in a list called Value, using the following code:
Value = [0.0] * arms
- Then, we print the Value list to the console, making sure all of the values are 0.0.
The first section of code initialized our rewards, number of arms, learning rate, and value list. Now, we need to implement the training cycle where our agent/algorithm will learn the value of each pull. Let's jump back into the code for Chapter_1_1.py and look to the next section:
- The next section of code in the listing we want to focus on is entitled agent learns and is shown here for reference:
# agent learns
for i in range(0, episodes):
action = random.randint(0,arms-1)
Value[action] = Value[action] + learning_rate * (
reward[action] - Value[action])
print(Value)
- We start by first defining a for loop that loops through 0 to our number of episodes. For each episode, we let the agent pull an arm and use the reward from that pull to update its determination of value for that action or arm.
- Next, we want to determine the action or arm the agent pulls randomly using the following code:
action = random.randint(0,arms-1)
- The code just selects a random arm/action number based on the total number of arms on the bandit (minus one to allow for proper indexing).
- This then allows us to determine the value of the pull by using the next line of code, which mirrors very well our previous value equation:
Value[action] = Value[action] + learning_rate * ( reward[action] - Value[action])
- That line of code clearly resembles the math for our previous Value equation. Now, think about how learning_rate is getting applied during each iteration of an episode. Notice that, with a rate of .1, our agent is learning or applying 1/10th of what reward the agent receives minus the Value function the agent previously equated. This little trick has the effect of averaging out the values across the episodes.
- Finally, after the looping completes and all of the episodes are run, we print the updated Value function for each action.
- Run the code from the command line or your favorite Python editor. In Visual Studio, this is as simple as hitting the play button. After the code has completed running, you should see something similar to the following, but not the exact output:
Output from Chapter_1_1.py
You will most certainly see different output values since the random action selections on your computer will be different. Python has many ways to set static values for random seeds but that isn't something we want to worry about quite yet.
Now, think back and compare those output values to the rewards set for each arm. Are they the same or different and if so, by how much? Generally, the learned values after only 100 episodes should indicate a clear value but likely not the finite value. This means the values will be smaller than the final rewards but they should still indicate a preference.
The solution we show here is an example of trial and error learning; it's that first thread we talked about back in the history of RL section. As you can see, the agent learns by randomly pulling an arm and determining the value. However, at no time does our agent learn to make better decisions based on those updated values. The agent always just pulls randomly. Our agent currently has no decision mechanism or what we call a policy in RL. We will look at how to implement a basic greedy policy in the next section.