Multiple logistic regression
In a similar fashion as with the multiple linear regression, the multiple logistic regression is about using more than one independent variable. Let us try combining the sepal length and the sepal width. Remember that we need to pre-process the data a little bit:
df = iris.query(species == ('setosa', 'versicolor'))
y_1 = pd.Categorical(df['species']).codes
x_n = ['sepal_length', 'sepal_width']
x_1 = df[x_n].valuesThe boundary decision
Feel free to skip this section and jump to the model implementation if you are not much interested in how we can derive the boundary decision.
From the model, we have the following:
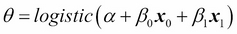
And from the definition of the logistic function, we have 
, when the argument of the logistic regression is zero, that is:
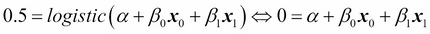
Reordering, we find the value of 
for which corresponds to the following expression:
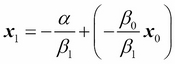
This expression for the boundary decision has the same mathematical form as a line equation, with the first term being the intercept and the second the...
