The bisection method
The bisection method is considered the simplest one-dimensional root-finding algorithm. The general interest is to find the value  of a continuous function
of a continuous function  such that
such that  .
.
Suppose we know the two points of an interval  and
and  , where
, where  , and that
, and that  and
and  lie along the continuous function, taking the midpoint of this interval as
lie along the continuous function, taking the midpoint of this interval as  , where
, where  , the bisection method then evaluates this value as f(c).
, the bisection method then evaluates this value as f(c).
Let's illustrate the setup of points along a nonlinear function with the following graph:
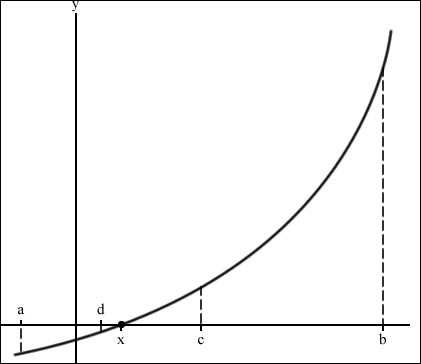
Since the value of f(a) is negative and f(b) is positive, the bisection method assumes that the root  lies somewhere between a and b and gives
lies somewhere between a and b and gives  .
.
If  or is very close to zero by some predetermined error tolerance value, then a root is declared as found. If
or is very close to zero by some predetermined error tolerance value, then a root is declared as found. If  , then we may conclude that a root exists along the interval
, then we may conclude that a root exists along the interval  and
and  , or interval
, or interval  and
and  otherwise.
otherwise.
On the next evaluation,  is replaced as either
is replaced as either  or
or  accordingly. With the new interval shortened, the bisection method repeats with the same evaluation to determine...
accordingly. With the new interval shortened, the bisection method repeats with the same evaluation to determine...
































































