Recall from Chapter 10, The Perceptron that while some Boolean functions such as AND, OR, and NAND can be approximated by the perceptron, the linearly inseparable function XOR cannot, as shown in the following plots:
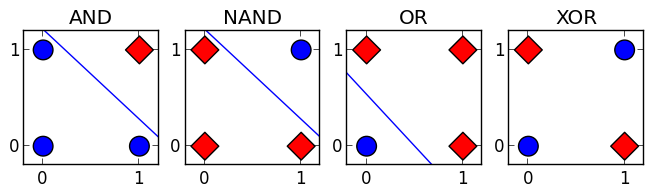
Let's review XOR in more detail to develop an intuition of the power of ANN. In contrast to AND, which outputs 1 when both of its inputs are equal to 1, and OR, which outputs 1 when at least one of the inputs are equal to 1, the output of XOR is 1 when exactly one of its inputs is equal to 1. We can view XOR as outputting 1 when two conditions are true. The first condition is that at least one of the inputs must be equal to 1; this is the same condition that OR tests. The second condition is that the inputs cannot both equal 1; NAND tests this condition. We can produce the same output as XOR by processing the input with both...



























































