Probability revisited
Many basic concepts of probability are detailed in Appendix B, Probability. Some of the key ideas in probability theory form the building blocks of probabilistic graph models. A good grasp of the relevant theory can help a great deal in understanding PGMs and how they are used to make inferences from data.
Concepts in probability
In this section, we will discuss important concepts related to probability theory that will be used in the discussion later in this chapter.
Conditional probability
The essence of conditional probability, given two related events a and ß, is to capture how we assign a value for one of the events when the other is known to have occurred. The conditional probability, or the conditional distribution, is represented by P(a | ß), that is, the probability of event a happening given that the event ß has occurred (equivalently, given that ß is true) and is formally defined as:
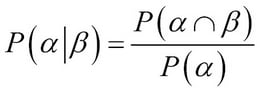
The P(a n ß) captures the events where both a and ß occur.












































































