Unifying model-based and model-free approaches

When we went from dynamic programming-based approaches to Monte Carlo and temporal-difference methods in Chapter 5, Solving the Reinforcement Learning Problem, our motivation was that it is limiting to assume that the environment transition probabilities are known. Now that we know how to learn the environment dynamics, we will leverage that to find a middle ground. It turns out that with a learned model of the environment, the learning with model-free methods can be accelerated. To that end, in this section, we first refresh our minds on Q-learning, then introduce a class of methods called Dyna.

Refresher on Q-learning

Let's start with remembering the definition of the action-value function:

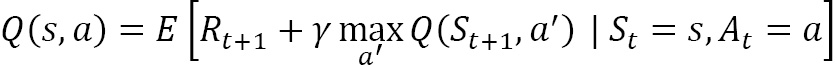
The expectation operator here is because the transition into the next state is probabilistic, so is a random variable along with . On the other hand, if we know the probability distribution of and , we can...