Let's see how convolution is done with color images, and how we can obtain multi-dimensional output matrices.
As we saw previously, a color image is represented as a three-dimensional matrix of numbers:
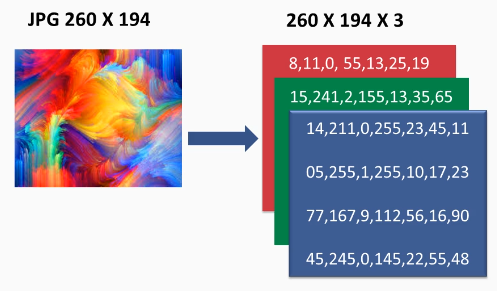
The third dimension is usually called all the channels. In this case, we have three channels: red, green, and blue. Considering how the convolution was done with the grayscale images, just convolving a two-dimensional matrix with one filter, one reasonable thing to do here—since we have three of the two-dimensional matrices—is to convolve with three filters:
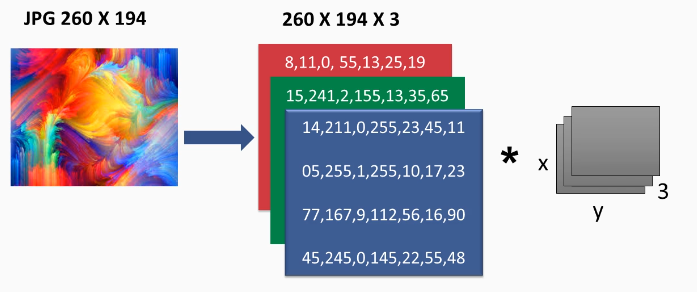
Each of these filters will be convolved with one of the channels.
So far, we've seen 3 x 3 filters, but actually, the two dimensions can vary from x to ε.
This kind of operation will now produce three outputs:
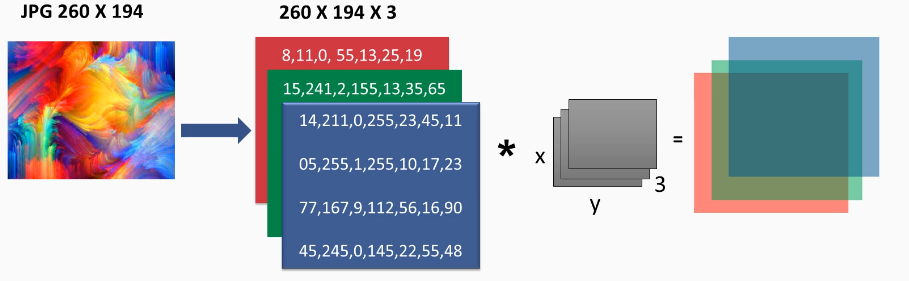
Let's look in a bit more detail at what's happened...


























































