Complex optimization algorithms
The nature of the objective function helps select the algorithm to be considered for the optimization of a given business problem. The more information that is available about the function, the easier it is to optimize the function. Of most importance is the fact that the objective function can be differentiated at any point in the search space.
Differentiability of objective functions
A differentiable objective function is one for which the derivative can be calculated at any given point in input space. The derivative (slope) is the rate of change of the function at that point. The Hessian is the rate at which the derivative of the function changes. Calculus helps optimize simple differentiable functions analytically. For differentiable objective functions, gradient-based optimization algorithms are used. However, there are objective functions for which the derivative cannot be computed, typically for very complex (noisy, multimodal, etc.) functions, which are called non-differentiable objective functions. There can be discontinuous objective functions as well, for which the derivatives can only be calculated in some regions of the search space. Stochastic and population algorithms handle such functions and are, hence, sometimes called black-box algorithms.
When an analytical form of the objective function is not available, one generally uses simulation-based optimization methods. The next subsection talks briefly about the algorithms considered while finding a feasible solution is challenging using classical methods, and they either compute or build around assumptions about the derivatives of objective functions.
Direct and stochastic algorithms
Direct and stochastic optimization algorithms are used in problems where the derivative of the objective function is unknown or cannot be calculated, that is, the search space is discontinuous. The former algorithms are deterministic and assume the objective function is unimodal (it has a single global optimum). Direct search is often referred to as pattern search as it effectively navigates through the search space using geometric shapes. Gradient information is approximated from the objective function and used in initiating a line search in the search space, eventually (with repeated line searches) triangulating the region of optimum. Powell’s method is one example of a direct search algorithm. It is a gradient-free method because the function to be optimized with it is non-differentiable.
On the other hand, stochastic algorithms make use of randomness in the global search, hence the name. These typically involve sampling the objective function and can handle problems with deceptive local optima. Simulated annealing (Figure 10.6) is an example of a stochastic search algorithm, that is, of global optimization, which occasionally accepts poorer initial configurations. Simulated annealing is a probabilistic technique used to solve unconstrained and bound-constrained optimization problems. It is a metaheuristic to approximate global optimization in a large search space of a physical process wherein the system energy is minimized.
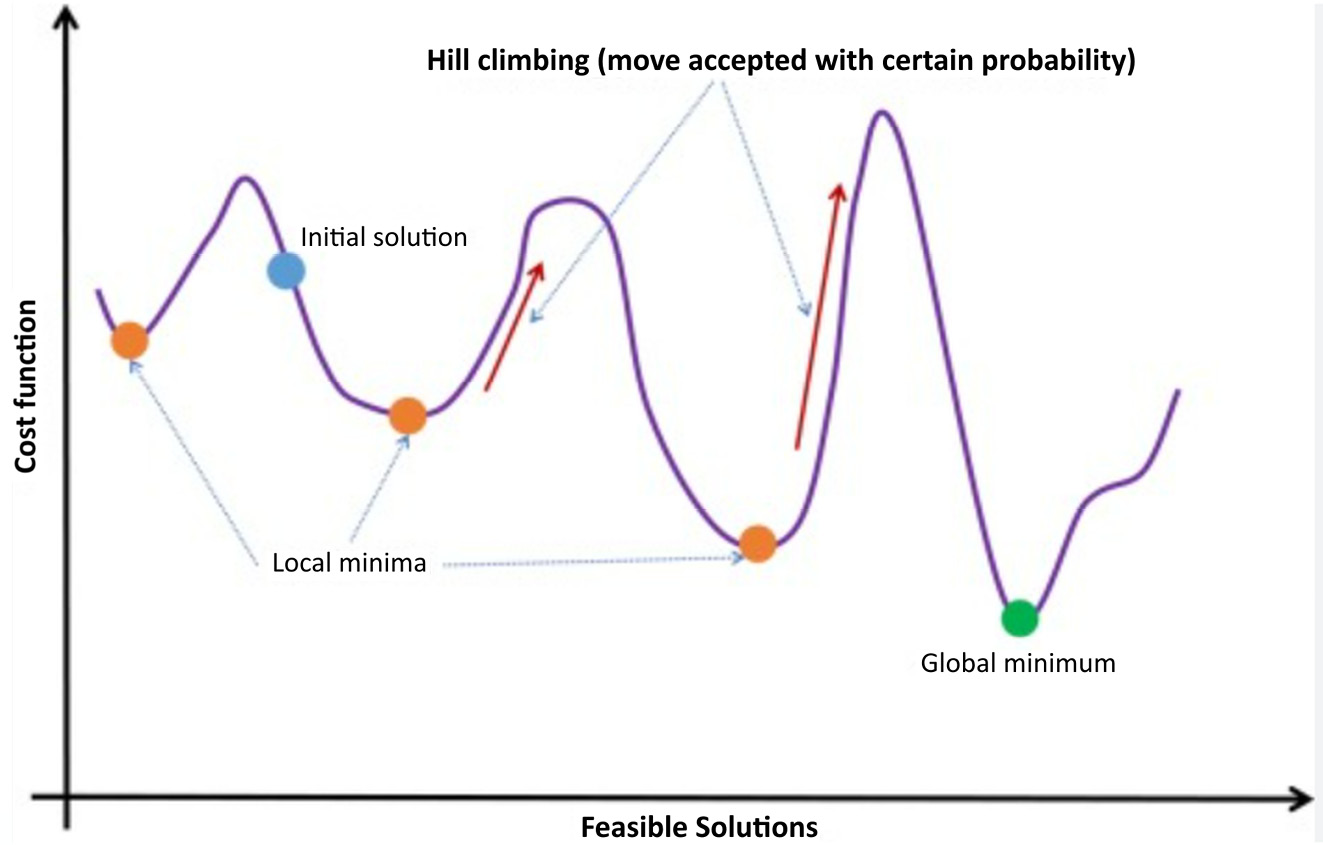
Figure 10.6: Simulated annealing is a stochastic optimization algorithm
Population optimization algorithms such as GAs are also stochastic and typically used for multimodal objective functions with multiple global optima and not-so-smooth (highly noisy) functions. These algorithms maintain a population of candidate solutions that add robustness to the search, thereby increasing the likelihood of overcoming local optima. The efficiency of these is very sensitive to the variables used in describing the problem. As with other heuristic algorithms, evolutionary algorithms have many degrees of freedom and, therefore, are difficult to tune for good model performance.
A GA pursues the evolution analogy, which proceeds by maintaining an even number of individuals in the population. These individuals make a generation, and a new generation is produced by randomly selecting a pair wherein the fitter individual is more likely to be chosen. GA is used to solve complex optimization problems by initialization (of the population), fitness assignment (to individuals in the population), and selection of the best (recombined) solution to the problem. A large community of researchers is working on GAs for utilization in most practical problems.























































