Detecting outliers using a z-score
The z-score is a common transformation for standardizing data. This is common when you want to compare different datasets. For example, it is easier to compare two data points from two different datasets relative to their distributions. This can be done because the z-score standardizes the data to be centered around a zero mean and the units represent standard deviations away from the mean. For example, in our dataset, the unit is measured in daily taxi passengers (in thousands). Once you apply the z-score transformation, you are no longer dealing with the number of passengers, but rather, the units represent standard deviation, which tells us how far an observation is from the mean. Here is the formula for the z-score:
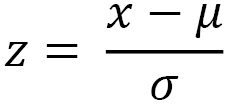
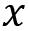
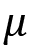
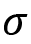
Keep in mind that the z-score is a lossless transformation, which means you will not lose...































































