7.6 Professor Hadamard, meet Professor Pauli

Other than mapping the state of a qubit to a Bloch sphere and looking at it differently, what can you do with a qubit? This section looks at the operations, also called gates, which you can apply to a single qubit. Later, we expand our exploration to gates with multiple qubits as inputs and outputs. In Chapter 9, “Wiring Up the Circuits,” we build circuits with these gates to implement algorithms. gate$quantum gate$reversible

Here, for example, is a circuit with one qubit initialized to |0⟩ that performs one operation, X, and then measures the qubit. The result of the measurement is |m₀⟩.

Quantum gates are always reversible, but some other operations are not. Quantum gates correspond to unitary transformations. Measurement is irreversible, and so is the |0⟩ RESET operation described in section 7.6.14. operation$measurement operation$|0⟩ RESET`gate-style |0⟩ RESET`gate-style

When I include the measurement operation in a circuit in the next chapter and beyond, it looks like this: qubit$measurement measurement

Measurement returns a |0⟩ or |1⟩. Mathematically, we do not worry about how it happens other than the probability.

Since a qubit state is a two-dimensional complex ket or vector, all quantum gates have 2-by-2 matrices with complex entries relative to some basis. This makes them small and very easy to manipulate. They are unitary matrices.

If A is a complex square matrix, then it is unitary if its adjoint A^† is also its inverse A^–1. Hence AA^† = A^† A = I. The columns of A are orthonormal, as are the rows. matrix$unitary

|det(A)| = 1. This equality says the absolute value of the determinant is 1, not that the determinant is 1. Since it is a unit in C, the determinant is e^φi for 0 ≤ φ < 2π.

The remainder of this section is a catalog of the most useful and commonly used 1-qubit quantum gates. As you will see, there is often more than one way to accomplish the same qubit state change. Why you would want to do so is the topic of Chapter 9, “Wiring Up the Circuits.”

7.6.1 The quantum ID gate

The ID gate does nothing, but we typically employ it when constructing or drawing circuits to show something happening to every qubit at every step. We can represent it by multiplication by I₂, the 2-by-2 identity matrix. I₂ is both unitary and Hermitian. gate$ID`gate-style ID`gate-style

When I include the ID gate in a circuit, it looks like this:

We also put the ID gate in a circuit to indicate a place to pause or delay. Its presence allows, for example, researchers to calculate measurements of the decoherence of a qubit.

7.6.2 The quantum X gate

The X gate has the matrix gate$X`gate-style X`gate-style σ_x`italic matrix$σ<sub>x</sub> σ<sub>0</sub>`italic matrix$σ₀

and this is the Pauli X matrix, named after Wolfgang Pauli, who won the Nobel Prize in Physics in 1945 (Figure 7.14). σ_x is both unitary and Hermitian. I often use the same name (in this case, X) for both the gate and its matrix in the standard basis kets. When we are not considering the matrix with respect to a specific basic, we refer to the X operator. Pauli, Wolfgang Pauli$matrix matrix$Pauli operator$Pauli

We also consider I₂ a Pauli matrix and refer to it as σ₀.

Figure 7.14: The physicist Wolfgang Pauli, 1900–1958

It has the property that

It “flips” between |0⟩ and |1⟩. The classic not gate is gate$not`gate-style not`gate-style

The not gate is a “bit flip,” and, by analogy, we also say X is a bit flip. gate$bit flip

For |ψ⟩ = a|0⟩ + b|1⟩ in C²,

X reverses the probabilities of measuring |0⟩ and |1⟩.

In terms of the Bloch sphere, the X gate rotates by π around the x-axis. So, the poles are flipped, and points in the lower hemisphere move to the upper, and vice versa.

Since X ○ X = ID, the X gate is its own inverse. This is reasonable because, in the classical case, it is also true that not ○ not is the identity operation.

When we considered rotations, we saw that the matrix for R³ that does a rotation around the x-axis by θ radians works like rotation

Plugging in θ = π, the rotation matrix is

In R³ standard coordinates, |0⟩ = (0, 0, 1) and |1⟩ = (0, 0, –1). Applying the rotation matrix, we get:

You can see this flipped |0⟩ and |1⟩. What about |+⟩ and |–⟩?

As you would expect from looking at the geometry of the Bloch sphere, it leaves these alone.

Exercise 7.18

What does the X gate do to |i⟩ and |–i⟩?

Exercise 7.19

What are the eigenvectors and eigenvalues of σ_x in C² relative to the standard basis?

When I include the X gate in a circuit, it looks like this:

You may also see it shown in some literature and software tools as a circle surrounding a plus sign:

The horizontal line, called a wire, represents the qubit and its state. The input state enters on the left, the X unitary transformation is applied, and the new quantum state result comes out on the right side. wire

7.6.3 The quantum Z gate

The Z gate has the matrix gate$Z`gate-style Z`gate-style σ_z`italic matrix$σ_z

and this is the Pauli Z matrix. It rotates qubit states by π around the z-axis on the Bloch sphere. σ_z is both unitary and Hermitian. Pauli$matrix matrix$Pauli operator$Pauli

The Z gate swaps |+⟩ and |–⟩ as well as |i⟩ and |–i⟩. It leaves |0⟩ and |1⟩ alone on the Bloch sphere.

Since Z ○ Z = ID, the Z gate is its own inverse. If you rotate by π and then rotate by π again, you end up back where you started.

For |ψ⟩ = a|0⟩ + b|1⟩ in C²,

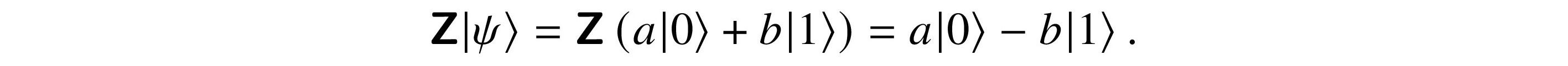
The probabilities of measuring |0⟩ and |1⟩ do not change after applying Z.

In C², σ_z has eigenvalues +1 and –1 for eigenvectors |0⟩ and |1⟩, respectively. Per section 7.3.4, Z or σ_z is the observable for the standard computational basis |0⟩ and |1⟩.

Remember that |1⟩ and –|1⟩ = e^πi |1⟩ in C² map to the same point we are also calling |1⟩ on the Bloch sphere because they differ only by multiplication by a unit, –1 = e^πi. If we express

then

We change the relative phase of |ψ⟩ to π plus that relative phase, adjusted to be between 0 and2π. This is a phase flip, and we call Z a phase flip gate. Since it reverses the sign of the second amplitude, it is also called a sign flip gate. gate$phase flip phase$flip gate$sign flip

When I include the Z gate in a circuit, it looks like this:

Exercise 7.20

Show by calculation that X ○ Z = – Z ○ X.

7.6.4 The quantum Y gate

The Y gate has the matrix gate$Y`gate-style Y`gate-style σ_y`italic matrix$σ_y

and this is the Pauli Y matrix. It rotates qubit states by π around the y-axis on the Bloch sphere. σ_y is both unitary and Hermitian. Pauli$matrix matrix$Pauli operator$Pauli

It swaps |0⟩ and |1⟩ and so is a bit flip. It also interchanges |+⟩ and |–⟩ but leaves |i⟩ and |–i⟩ alone.

Since Y ○ Y = ID, the Y gate is its own inverse.

For |ψ⟩ = a|0⟩ + b|1⟩ in C²,

From this, we can see that Y simultaneously does a bit flip and a phase flip. In C², σ_y has eigenvalues +1 and –1 for eigenvectors |i⟩ and |–i⟩, respectively.

If |ψ⟩ = a|0⟩ + b|1⟩ in C², then a bit flip interchanges the coefficients of |0⟩ and |1⟩. A phase flip changes the sign of the coefficient of |1⟩. A simultaneous bit and phase flip does both:

When I include the Y gate in a circuit, it looks like this:

Exercise 7.21

What is the 3-by-3 rotation matrix for the Y gate?

Exercise 7.22

Show by calculation that X ○ Y = –Y ○ X and Z ○ Y = –Y ○ Z.

7.6.5 The quantum H gate

The H gate, or H^⊗1 or Hadamard gate, has the matrix gate$H`gate-style gate$H<sup>⊗1</sup>`gate-style gate$Hadamard H`gate-style gate$H<sup>⊗1</sup>`gate-style

operating on C².

By matrix multiplication,

By linearity,

Exercise 7.23

Show that H |–⟩ = |1⟩.

The Hadamard gate, named after Jacques Hadamard (Figure 7.15), is one of the most frequently used gates in quantum computing. H is often the first gate applied in a circuit. When you read “put the qubit in superposition,” it usually means “take the qubit initialized in the |0⟩ state and apply H to it.”

Figure 7.15: The mathematician Jacques Hadamard, 1865–1963

The Hadamard matrix is the change of basis matrix from {|0⟩, |1⟩} to {|+⟩, |–⟩}. Since H ○ H = ID, the H gate is its own inverse. basis$change of

A change of basis from the computational basis {|0⟩, |1⟩} to the Hadamard basis {|+⟩, |–⟩} changes a bit flip X to a phase flip Z. basis$Hadamard

When I include the H gate in a circuit, it looks like this:

Consider |b⟩, where b is 0 or 1. The expression (–1)^b is 1 when b = 0 and –1 when b = 1.

For our H gate, we look at

and notice that

When b = 0, we have |0⟩ going to √2/2 (|0⟩ + |1⟩). For b = 1, we end up with √2/2 (|0⟩ – |1⟩).

Exercise 7.24

Using matrix calculations, show that X = H ○ Z ○ H.

Exercise 7.25

What is H ○ X ○ H?

Exercise 7.26

What is the 3-by-3 matrix for the H gate on the Bloch sphere? It is the product of two 3-by-3 rotation matrices. What are they?

7.6.6 The quantum R_φ^z gates

We can generalize the phase-changing behavior of the Z gate by noting gate$R_φ^z`gate-style gate$R<sub>φ</sub><sup>z</sup>`gate-style

This last form is the template for the collection of gates given the name R_φ^z:

|1⟩ is an eigenvector of R_φ^z with eigenvalue e ^φi.

This collection is infinite as φ can take on any radian value greater than or equal to 0 and less than 2π. These gates change the phase of a qubit state by φ. This is a parameterized z-rotation gate, with φ being the parameter. gate$parameterized

Exercise 7.27

What is the 3-by-3 rotation matrix for R_φ^z? For Z?

The inverse of R_φ^z is R_2π-φ^z. R₀^z = ID. R_π^z = Z.

When I include the R_φ^z gate in a circuit for a particular value of φ, it looks like this:

Since

an alternative form of the matrix for R_φ^z up to a global phase change is

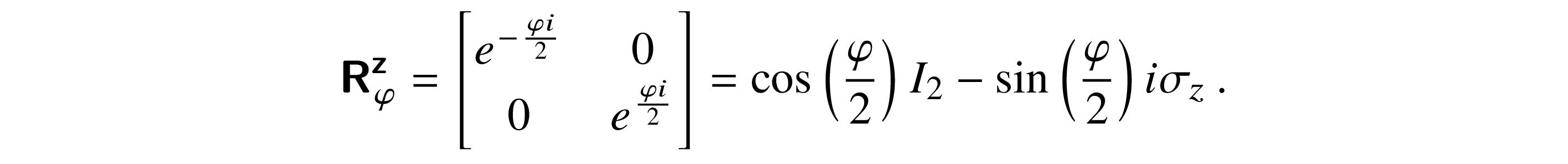
e^φi/2 is a complex unit, and multiplication by it is not observable when we measure.

7.6.7 The quantum S gate

The S gate is a shorthand for R_π/2^z. After applying, we adjust the phase to be greater than or equal to 0 and less than 2π: gate$S`gate-style S`gate-style

|1⟩ is an eigenvector of S with eigenvalue i.

Exercise 7.28

What is the 3-by-3 rotation matrix for the S gate?

When I include the S gate in a circuit, it looks like this:

Traditionally and confusingly, the S gate is also known as the π/4 gate. This is because we can express the matrix in this way: gate$π/4

The unit factor e^πi/4 in front does not have an observable effect on the quantum state of the result of applying S. Some authors call S “the phase gate,” but I won’t. gate$phase phase gate

7.6.8 The quantum S^† gate

The S^† (pronounced “S dagger”) gate is a shorthand for R_3π/2^z = R_–π/2^z. After applying, we adjust the phase to be greater than or equal to 0 and less than 2π: gate$S^†`gate-style S<sup>†</sup>`gate-style

|1⟩ is an eigenvector of S^† with eigenvalue –i.

The gate gets its name because the matrix for S^† is the adjoint of the S matrix:

Exercise 7.29

What is the 3-by-3 rotation matrix for the S^†?

When I include the S^† gate in a circuit, it looks like this:

7.6.9 The quantum T gate

The T gate is a shorthand for R_π/4^z. After applying, we adjust the phase to be greater than or equal to 0 and less than 2π: gate$T`gate-style T`gate-style

|1⟩ is an eigenvector of T with eigenvalue √2/2 + √2/2i.

Exercise 7.30

What is the 3-by-3 rotation matrix for the T gate?

We can get the S by applying the T twice: S = T ○ T.

When I include the T gate in a circuit, it looks like this:

The T gate is also known as the π/8 gate. We can write its matrix as gate$π/8

The unit factor e^πi/8 in front does not have an observable effect on the quantum state of the result of applying T.

7.6.10 The quantum T^† gate

The T ^† gate (pronounced “T dagger”) is a shorthand for R_7π/4^z = R_–π/4^z. After applying, we adjust the phase to be greater than or equal to 0 and less than 2π: gate$T^†`gate-style T<sup>†</sup>`gate-style

|1⟩ is an eigenvector of T ^† with eigenvalue √2/2 – √2/2i.

It gets its name because the matrix for T ^† is the adjoint of the T matrix:

Exercise 7.31

What is the 3-by-3 rotation matrix for the T ^† gate?

We can get the T^† by applying the T ^† twice: S^† = T ^† ○ T ^†.

When I include the T ^† gate in a circuit, it looks like this:

7.6.11 The quantum Ph_φ global phase gate

Our next 1-qubit parameterized gate is the global phase gate Ph_φ: gate$Ph`gate-style Ph`gate-style

Ph_φ has no observable effect on the qubit when it is measured.

Exercise 7.32

What gate do you get when φ = 0?

Exercise 7.33

How does this differ from the R_φ^z gate?

When I include the Ph_φ gate in a circuit, it looks like this:

7.6.12 The quantum R_φ^x and R_φ^y gates

Just as R_φ^z is an arbitrary rotation around the z-axis, we can define gates that rotate around the x- and y-axes: gate$R_φ^x`gate-style gate$R<sub>φ</sub><sup>x</sup>`gate-style gate$R_φ^y`gate-style gate$R<sub>φ</sub><sup>y</sup>`gate-style

and

These are parameterized x- and y-rotation gates, with φ being the parameter. gate$parameterized

When I include these gates in circuits, they look like this:

Exercise 7.34

Show that H = X ○ R_π/2^y.

7.6.13 The quantum √NOT gate

Another gate used in the quantum computing literature is the “square root of NOT” gate. It has the matrix gate$√NOT`gate-style √NOT`gate-style

Squaring this, √NOT ○ √NOT, we get

The X gate is the quantum version of not, and that’s how this gate gets its name.

Exercise 7.35

Show that √NOT is unitary. What is its determinant? What does it do to |0⟩ and |1⟩?

When I include this gate in a circuit, it looks like this:

The adjoint of this gate has the matrix

Exercise 7.36

What is the square of the adjoint of the “square root of NOT” gate?

When I include this gate in a circuit, it looks like this:

Exercise 7.37

What are the matrices for the √Y and √Z gates? gate$√Y`gate-style √Y`gate-style gate$√Z`gate-style √Z`gate-style

7.6.14 The quantum |0⟩ RESET operation

Though it is not a reversible unitary operation, and hence, not a gate, some quantum computing software environments allow you to reset a qubit in the middle of a circuit to |0⟩. This operation, denoted |0⟩ RESET, is convenient if you use a qubit as a temporary scratchpad for multiple values within an algorithm. operation$|0⟩ RESET`gate-style |0⟩ RESET`gate-style

This operation may make your code nonportable across different quantum computing architectures and software development kits.

When I include this operation in a circuit, it looks like this: