Spanning tree
A spanning tree T of a graph G is a subgraph that is a tree and must contain all the vertices of G. In order to fulfill this condition, G must be a connected graph (that is, all vertices have at least one connection to another vertex).
Take a look at the following example of a graph and its spanning trees:
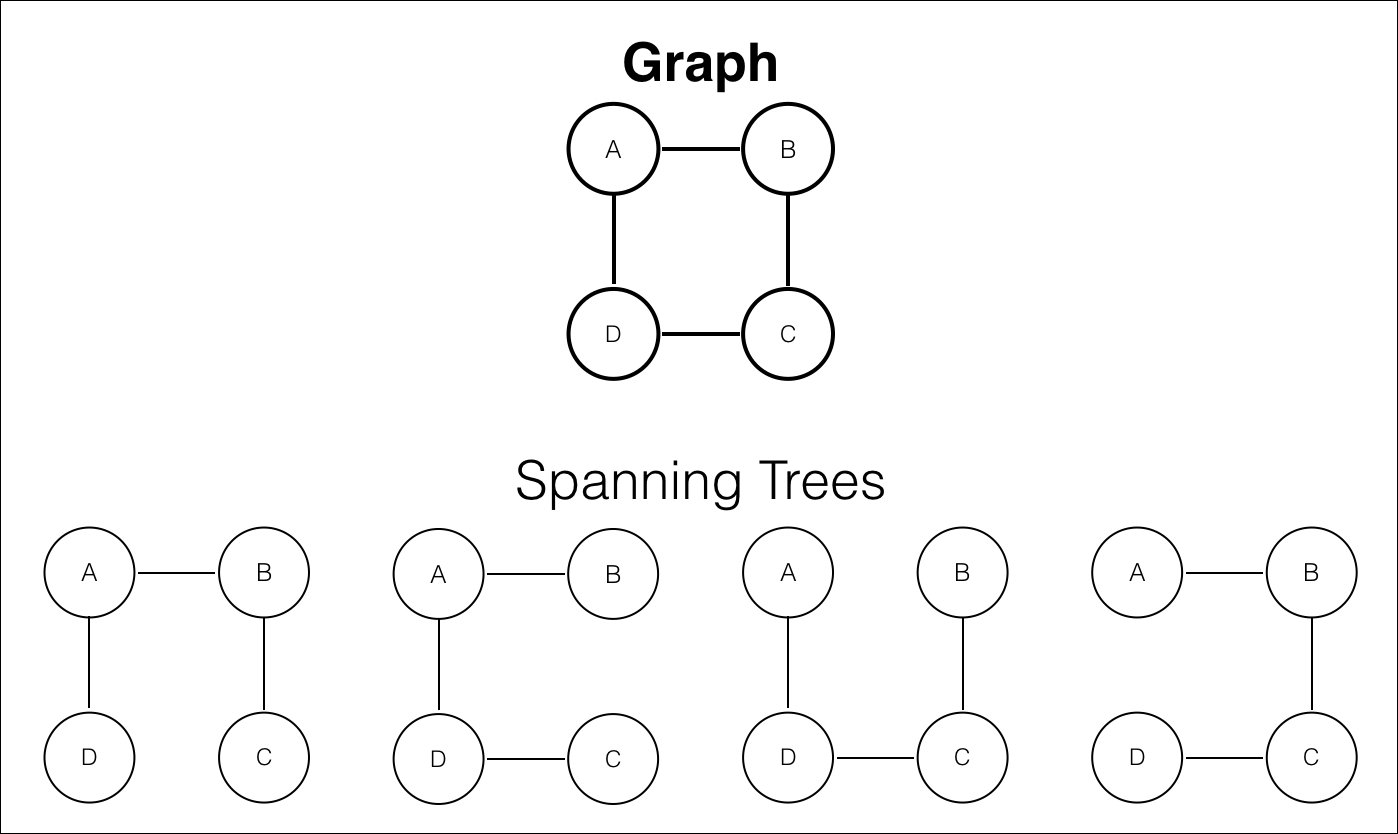
A graph and its spanning trees example
Note that there could be more than one spanning tree for any graph G. If graph G is a tree, then there is only one spanning tree, which is the tree itself:
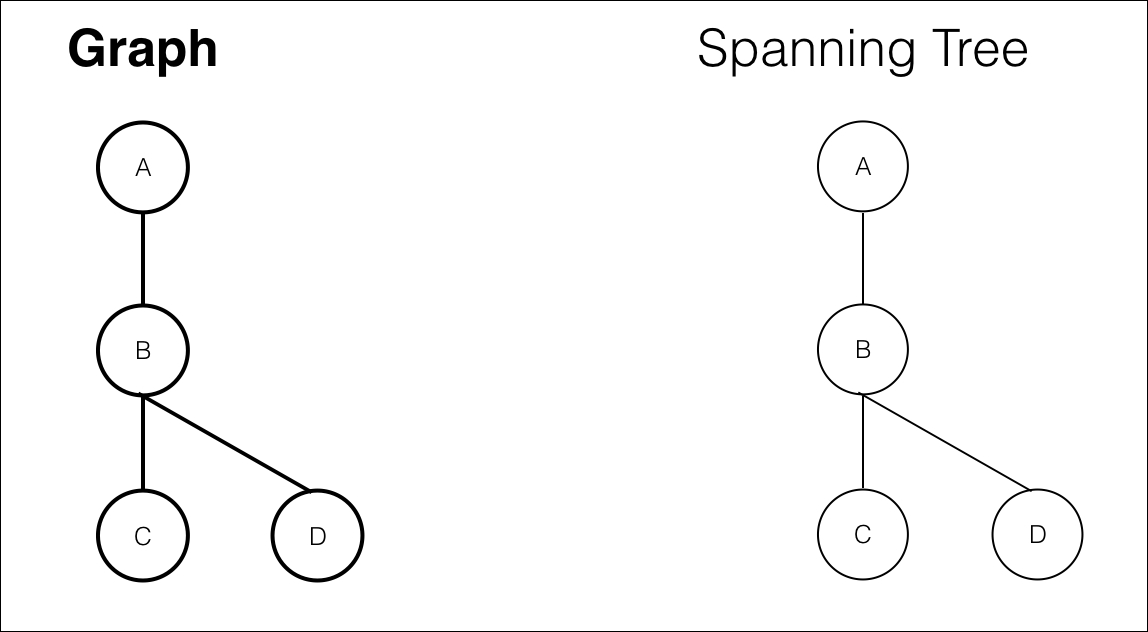
A tree and its spanning tree example
Remember the BFS and DFS algorithms? Well, both of them will give us one of the spanning trees of a graph.
Spanning tree applications include several examples, such as pathfinding algorithms (such as Dijkstra and A*), speech recognition, Internet routing protocol techniques to avoid loops, and so on. Most of them make use at some point of the minimum spanning tree, which we are going to see next.
Minimum spanning tree
In some scenarios where we can...























































