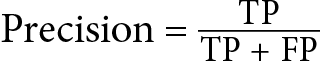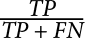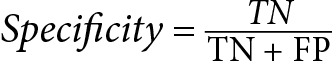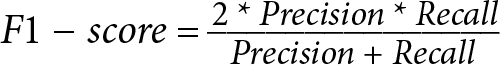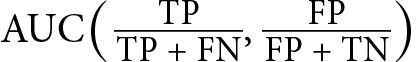Common evaluation metrics
Several machine learning and deep learning metrics are used for evaluating the performance of classification models.
Let’s look at some of the helpful metrics that can help evaluate the performance of our model on the test set.
Confusion matrix
Given a model that tries to classify an example as belonging to the positive or negative class, there are four possibilities:
- True Positive (TP): This occurs when the model correctly predicts a sample as part of the positive class, which is its actual classification
- False Negative (FN): This happens when the model incorrectly classifies a sample from the positive class as belonging to the negative class
- True Negative (TN): This refers to instances where the model correctly identifies a sample as part of the negative class, which is its actual classification
- False Positive (FP): This occurs when the model incorrectly predicts a sample from the negative class as belonging to the positive class
Table 1.1 shows in what ways the model can get “confused” when making predictions, aptly called the confusion matrix. The confusion matrix forms the basis of many common metrics in machine learning:
|
Predicted Positive |
Predicted Negative |
|
|
Actually Positive |
True Positive (TP) |
False Negative (FN) |
|
Actually Negative |
False Positive (FP) |
True Negative (TN) |
Table 1.1 – Confusion matrix
Let’s look at some of the most common metrics in machine learning:
- True Positive Rate (TPR) measures the proportion of actual positive examples correctly classified by the model:

- False Positive Rate (FPR) measures the proportion of actual negative examples that are incorrectly identified as positives by the model:
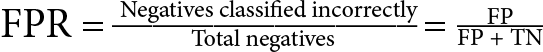
- Accuracy: Accuracy is the fraction of correct predictions made out of all the predictions that the model makes. This is mathematically equal to
 . This functionality is available in the
. This functionality is available in the sklearnlibrary assklearn.metrics.accuracy_score. - Precision: Precision, as an evaluation metric, measures the proportion of true positives over the number of items that the model predicts as belonging to the positive class, which is equal to the sum of the true positives and false positives. A high precision score indicates that the model has a low rate of false positives, meaning that when it predicts a positive result, it is usually correct. You can find this functionality in the
sklearnlibrary under the namesklearn.metrics.precision_score. .
. - Recall (or sensitivity, or true positive rate): Recall measures the proportion of true positives over the number of items that belong to the positive class. The number of items that belong to the positive class is equal to the sum of true positives and false negatives. A high recall score indicates that the model has a low rate of false negatives, meaning that it correctly identifies most of the positive instances. It is especially important to measure recall when the cost of mislabeling a positive example as negative (false negatives) is high.
Recall measures the model’s ability to correctly detect all the positive instances. Recall can be considered to be the accuracy of the positive class in binary classification. You can find this functionality in the
sklearnlibrary under the namesklearn.metrics.recall_score.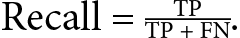
Table 1.2 summarizes the differences between precision and recall:
|
Precision |
Recall |
|
|
Definition |
Precision is a measure of trustworthiness |
Recall is a measure of completeness |
|
Question to ask |
When the model says something is positive, how often is it right? |
Out of all the positive instances, how many did the model correctly identify? |
|
Example (using an email filter) |
Precision measures how many of the emails the model flags as spam are actually spam, as a percentage of all the flagged emails |
Recall measures how many of the actual spam emails the model catches, as a percentage of all the spam emails in the dataset |
|
Formula |
|
|
Table 1.2 – Precision versus recall
Why can accuracy be a bad metric for imbalanced datasets?
Let’s assume we have an imbalanced dataset with 1,000 examples, with 100 labels belonging to class 1 (the minority class) and 900 belonging to class 0 (the majority class).
Let’s say we have a model that always predicts 0 for all examples. The model’s accuracy for the minority class is

Figure 1.7 – A comic showing accuracy may not always be the right metric
This brings us to the precision-recall trade-off in machine learning. Usually, precision and recall are inversely correlated – that is, when recall increases, precision most often decreases. Why? Note that recall  and for recall to increase, FN should decrease. This means the model needs to classify more items as positive. However, if the model classifies more items as positive, some of these will likely be incorrect classifications, leading to an increase in the number of false positives (FPs). As the number of FPs increases, precision, defined as
and for recall to increase, FN should decrease. This means the model needs to classify more items as positive. However, if the model classifies more items as positive, some of these will likely be incorrect classifications, leading to an increase in the number of false positives (FPs). As the number of FPs increases, precision, defined as  will decrease. With similar logic, you can argue that when recall decreases, precision often increases.
will decrease. With similar logic, you can argue that when recall decreases, precision often increases.
Next, let’s try to understand some of the precision and recall-based metrics that can help measure the performance of models trained on imbalanced data:
- F1 score: The F1 score (also called F-measure) is the harmonic mean of precision and recall. It combines precision and recall into a single metric. The F1 score varies between 0 and 1 and is most useful when we want to give equal priority to precision and recall (more on this later). This is available in the
sklearnlibrary assklearn.metrics.f1_score. - F-beta score or F-measure: The F-beta score is a generalization of the F1 score. It is a weighted harmonic mean of precision and recall, where the beta parameter controls the relative importance of precision and recall.
The formula for the F-beta
 score is as follows:
score is as follows:
Here, beta
 is a positive parameter that determines the weight given to precision in the calculation of the score. When beta
is a positive parameter that determines the weight given to precision in the calculation of the score. When beta  is set to 1, the F1 score is obtained, which is the harmonic mean of precision and recall. The F-beta score is a useful metric for imbalanced datasets, where one class may be more important than the other. By adjusting the beta parameter, we can control the relative importance of precision and recall for a particular class. For example, if we want to prioritize precision over recall for the minority class, we can set beta < 1. To see why that’s the case, set
is set to 1, the F1 score is obtained, which is the harmonic mean of precision and recall. The F-beta score is a useful metric for imbalanced datasets, where one class may be more important than the other. By adjusting the beta parameter, we can control the relative importance of precision and recall for a particular class. For example, if we want to prioritize precision over recall for the minority class, we can set beta < 1. To see why that’s the case, set  in the
in the  formula, which implies
formula, which implies  .
.Conversely, if we want to prioritize recall over precision for the minority class, we can set beta > 1 (we can set β = ∞ in the
 formula to see it reduce to recall).
formula to see it reduce to recall).In practice, the choice of beta parameter depends on the specific problem and the desired trade-off between precision and recall. In general, higher values of beta result in more emphasis on recall, while lower values of beta result in more emphasis on precision. This is available in the
sklearnlibrary assklearn.metrics.fbeta_score. - Balanced accuracy score: The balanced accuracy score is defined as the average of the recall obtained in each class. This metric is commonly used in both binary and multiclass classification scenarios to address imbalanced datasets. This is available in the
sklearnlibrary assklearn.metrics.balanced_accuracy_score. - Specificity (SPE): Specificity is a measure of the model’s ability to correctly identify the negative samples. In binary classification, it is calculated as the ratio of true negative predictions to the total number of negative samples. High specificity indicates that the model is good at identifying the negative class, while low specificity indicates that the model is biased toward the positive class.
- Support: Support refers to the number of samples in each class. Support is one of the values returned by the
sklearn.metrics.precision_recall_fscore_supportandimblearn.metrics.classification_report_imbalancedAPIs. - Geometric mean: The geometric mean is a measure of the overall performance of the model on imbalanced datasets. In
imbalanced-learn,geometric_mean_score()is defined by the geometric mean of “accuracy on positive class examples” (recall or sensitivity or TPR) and “accuracy on negative class examples” (specificity or TNR). So, even if one class is heavily outnumbered by the other class, the metric will still be representative of the model’s overall performance. - Index Balanced Accuracy (IBA): The IBA [1] is a measure of the overall accuracy of the model on imbalanced datasets. It takes into account both the sensitivity and specificity of the model and is calculated as the mean of the sensitivity and specificity, weighted by the imbalance ratio of each class. The IBA metric is useful for evaluating the overall performance of the model on imbalanced datasets and can be used to compare the performance of different models. IBA is one of the several values returned by
imblearn.metrics.classification_report_imbalanced.
Table 1.3 shows the associated metrics and their formulas as an extension of the confusion matrix:
|
Predicted Positive |
Predicted Negative |
||
|
Actually Positive |
True positive (TP) |
False negative (FN) |
Recall = Sensitivity = True positive rate (TPR) = |
|
Actually Negative |
False positive (FP) |
True negative (TN) |
|
|
Precision = TP/(TP+FP) FPR = FP/(FP+TN) |
|
Table 1.3 – Confusion matrix with various metrics and their definitions
ROC
Receiver Operating Characteristics, commonly known as ROC curves, are plots that display the TPR on the y-axis against the FPR on the x-axis for various threshold values:
- The ROC curve essentially represents the proportion of correctly predicted positive instances on the y-axis, contrasted with the proportion of incorrectly predicted negative instances on the x-axis.
- In classification tasks, a threshold is a cut-off value that’s used to determine the class of an example. For instance, if a model classifies an example as “positive,” a threshold of 0.5 might be set to decide whether the instance should be labeled as belonging to the “positive” or “negative” class. The ROC curve can be used to identify the optimal threshold for a model. This topic will be discussed in detail in Chapter 5, Cost-Sensitive Learning.
- To create the ROC curve, we calculate the TPR and FPR for many various threshold values of the model’s predicted probabilities. For each threshold, the corresponding TPR value is plotted on the y-axis, and the FPR value is plotted on the x-axis, creating a single point. By connecting these points, we generate the ROC curve (Figure 1.8):

Figure 1.8 – The ROC curve as a plot of TPR versus FPR (the dotted line shows a model with no skill)
Some properties of the ROC curve are as follows:
- The Area Under Curve (AUC) of a ROC curve (also called AUC-ROC) serves a specific purpose: it provides a single numerical value that represents the model’s performance across all possible classification thresholds:
- AUC-ROC represents the degree of separability of the classes. This means that the higher the AUC-ROC, the more the model can distinguish between the classes and predict a positive class example as positive and a negative class example as negative. A poor model with an AUC near 0 essentially predicts a positive class as a negative class and vice versa.
- The AUC-ROC of a random classifier is 0.5 and is the diagonal joining the points (0,0) and (1,0) on the ROC curve.
- The AUC-ROC has a probabilistic interpretation: an AUC of 0.9 indicates a 90% likelihood that the model will assign a higher score to a randomly chosen positive class example than to a negative class example. That is, AUC-ROC can be depicted as follows:
 P(score(x+ ) > score(x− ))
P(score(x+ ) > score(x− ))
Here, 𝑥+ denotes the positive (minority) class, and 𝑥− denotes the negative (majority) class.
- In the context of evaluating model performance, it’s crucial to use a test set that reflects the distribution of the data the model will encounter in real-world scenarios. This is particularly relevant when considering metrics such as the ROC curve, which remains consistent regardless of changes in class imbalance within the test data. Whether we have 1:1, 1:10, or 1:100 as the minority_class: majority_class distribution in the test set, the ROC curve remains the same [2]. The reason for this is that both of these rates are independent of the class distribution in the test data because they are calculated only based on the correctly and incorrectly classified instances of each class, not the total number of instances of each class. This is not to be confused with the change in imbalance in the training data, which can adversely impact the model’s performance and would be reflected in the ROC curve.
Now, let’s look at some of the problems in using ROC for imbalanced datasets:
- ROC does not distinguish between the various classes – that is, it does not emphasize one class more over the other. This can be a problem for imbalanced datasets where, often, the minority class is more important to detect than the majority class. Because of this, it may not reflect the minority class well. For example, we may want better recall over precision.
- While ROC curves can be useful for comparing the performance of models across a full range of FPRs, they may not be as relevant for specific applications that require a very low FPR, such as fraud detection in financial transactions or banking applications. The reason the FPR needs to be very low is that such applications usually require limited manual intervention. The number of transactions that can be manually checked may be as low as 1% or even 0.1% of all the data, which means the FPR can’t be higher than 0.001. In these cases, anything to the right of an FPR equal to 0.001 on the ROC curve becomes irrelevant [3]. To further understand this point, let’s consider an example:
- Let’s say that for a test set, we have a total of 10,000 examples and only 100 examples of the positive class, making up 1% of the examples. So, any FPR higher than 1% - that is, 0.01 – is going to raise too many alerts to be handled manually by investigators.
- The performance on the far left-hand side of the ROC curve becomes crucial in most real-world problems, which are often dominated by a large number of negative instances. As a result, most of the ROC curve becomes irrelevant for applications that need to maintain a very low FPR.
Precision-Recall curve
Similar to ROC curves, Precision-Recall (PR) curves plot a pair of metrics for different threshold values. But unlike ROC curves, which plot TPR and FPR, PR curves plot precision and recall. To demonstrate the difference between the two curves, let’s say we compare the performance of two models – Model 1 and Model 2 – on a particular handcrafted imbalanced dataset:
- In Figure 1.9 (a), the ROC curves for both models appear to be close to the top-left corner (point (0, 1)), which might lead you to conclude that both models are performing well. However, this can be misleading, especially in the context of imbalanced datasets.
- When we turn our attention to the PR curves in Figure 1.9 (b), a different story unfolds. Model 2 comes closer to the ideal top-right corner (point (1, 1)) of the plot, indicating that its performance is much better than Model 1 when precision and recall are considered.
- The PR curve reveals that Model 2 has an advantage over Model 1.
This discrepancy between the ROC and PR curves also underscores the importance of using multiple metrics for model evaluation, particularly when dealing with imbalanced data:

Figure 1.9 – The PR curve can show obvious differences between models compared to the ROC curve
Let’s try to understand these observations in detail. While the ROC curve shows very little difference between the performance of the two models, the PR curve shows a much bigger gap. The reason for this is that the ROC curve uses FPR, which is FP/(FP+TN). Usually, TN is really high for an imbalanced dataset, and hence even if FP changes by a decent amount, FPR’s overall value is overshadowed by TN. Hence, ROC doesn’t change by a whole lot.
The conclusion of which classifier is superior can change with the distribution of classes in the test set. In the case of skewed datasets, the PR curve can more clearly show that the model did not work well compared to the ROC curve, as shown in the preceding figure.
The average precision is a single number that’s used to summarize a PR curve, and the corresponding API in sklearn is sklearn.metrics.average_precision_score.
Relation between the ROC curve and PR curve
The primary distinction between the ROC curve and the PR curve lies in the fact that while ROC assesses how well the model can “calculate” both positive and negative classes, PR solely focuses on the positive class. Therefore, when dealing with a balanced dataset scenario and you are concerned with both the positive and negative classes, ROC AUC works exceptionally well. In contrast, when dealing with an imbalanced situation, PR AUC is more suitable. However, it’s important to keep in mind that PR AUC only evaluates the model’s ability to “calculate” the positive class. Because PR curves are more sensitive to the positive (minority) class, we will be using PR curves throughout the first half of this book.
We can reimagine the PR curve with precision on the x-axis and TPR, also known as recall, on the y-axis. The key difference between the two curves is that while the ROC curve uses FPR, the PR curve uses precision.
As discussed earlier, FPR tends to be very low when dealing with imbalanced datasets. This aspect of having low FPR values is crucial in certain applications such as fraud detection, where the capacity for manual investigations is inherently limited. Consequently, this perspective can alter the perceived performance of classifiers. As shown in Figure 1.9, it’s also possible that the performances of the two models seem reversed when compared using average precision (0.69 versus 0.90) instead of AUC-ROC (0.97 and 0.95).
Let’s summarize this:
- The AUC-ROC is the area under the curve plotted with TPR on the y-axis and FPR on the x-axis.
- The AUC-PR is the area under the curve plotted with precision on the y-axis and recall on the x-axis.
As TPR equals recall, the two plots only differ in what recall is compared to – either precision or FPR. Additionally, the plots are rotated by 90 degrees relative to each other:
|
AUC-ROC |
AUC-PR |
|
|
General formula |
AUC(TPR, FPR) |
AUC(Precision, Recall) |
|
Expanded formula |
|
|
|
Equivalence |
AUC(Recall, FPR) |
AUC(Precision, Recall) |
Table 1.4 – Comparing the ROC and PR curves
In the next few sections, we’ll explore the circumstances that lead to imbalances in datasets, the challenges these imbalances can pose, and the situations where data imbalance might not be a concern.