Covariance
One way of quantifying the strength of the relationship between two variables is their covariance. This measures the tendency of two variables to change together.
If we have two series, X and Y, their deviations from the mean are:

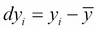
Where xi is the value of X at index i, yi is the value of Y at index i,  is the mean of X, and
is the mean of X, and  is the mean of Y. If X and Y tend to vary together, their deviations from the mean tend to have the same sign: negative if they're less than the mean, positive if they're greater. If we multiply them together, the product is positive when they have the same sign and negative when they have different signs. Adding up the products gives a measure of the tendency of the two variables to deviate from the mean in the same direction for each given sample.
is the mean of Y. If X and Y tend to vary together, their deviations from the mean tend to have the same sign: negative if they're less than the mean, positive if they're greater. If we multiply them together, the product is positive when they have the same sign and negative when they have different signs. Adding up the products gives a measure of the tendency of the two variables to deviate from the mean in the same direction for each given sample.
Covariance is defined as the mean of these products:
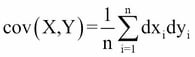
Covariance can be calculated in Clojure using the following code:
(defn covariance [xs ys]
(let [x-bar (s/mean xs)
y-bar (s/mean xs)
dx (map (fn...






























































