Bayes' theorem
The probability of an event E conditioned on evidence X is proportional to the prior probability of the event and the likelihood of the evidence given that the event has occurred. This is Bayes' Theorem:
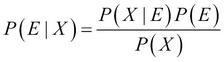
P(X) is the normalizing constant, which is also called the marginal probability of X. P(E) is the prior, and P(X|E) is the likelihood. P(E|X) is also called the posterior probability.
Bayes' Theorem expressed in terms of the posterior and prior odds is known as Bayes' Rule.
Density estimation
Estimating the hidden probability density function of a random variable from sample data randomly drawn from the population is known as density estimation. Gaussian mixtures and kernel density estimates are examples used in feature engineering, data modeling, and clustering.
Given a probability density function f(X) for a random variable X, the probabilities associated with the values of X can be found as follows:
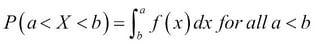
Density estimation can be parametric, where it is assumed...












































































