Linear algebra, at its core, is about solving a set of linear equations, referred to as a system of equations. A large number of problems can be formulated as a system of linear equations.
We have two equations and two unknowns, as follows:
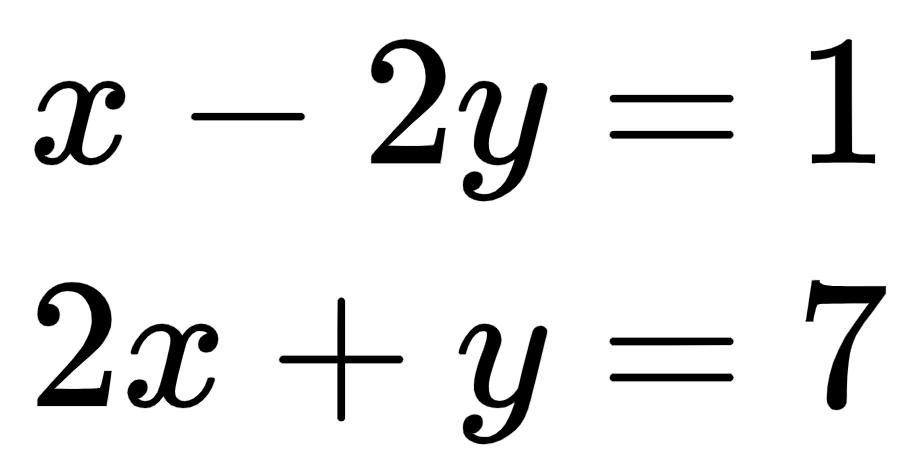
Both equations produce straight lines. The solution to both these equations is the point where both lines meet. In this case, the answer is the point (3, 1).
But for our purposes, in linear algebra, we write the preceding equations as a vector equation that looks like this:
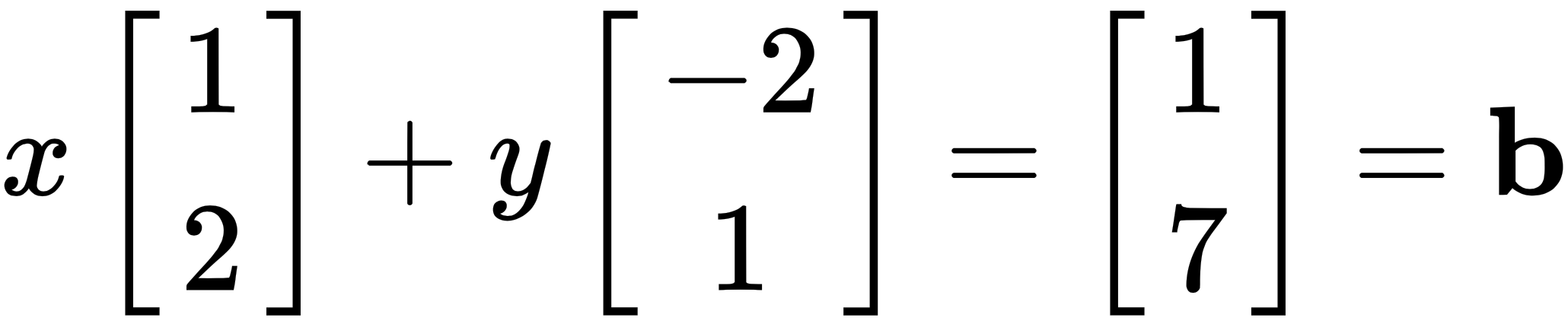
Here, b is the result vector.
Placing the point (3, 1) into the vector equation, we get the following:
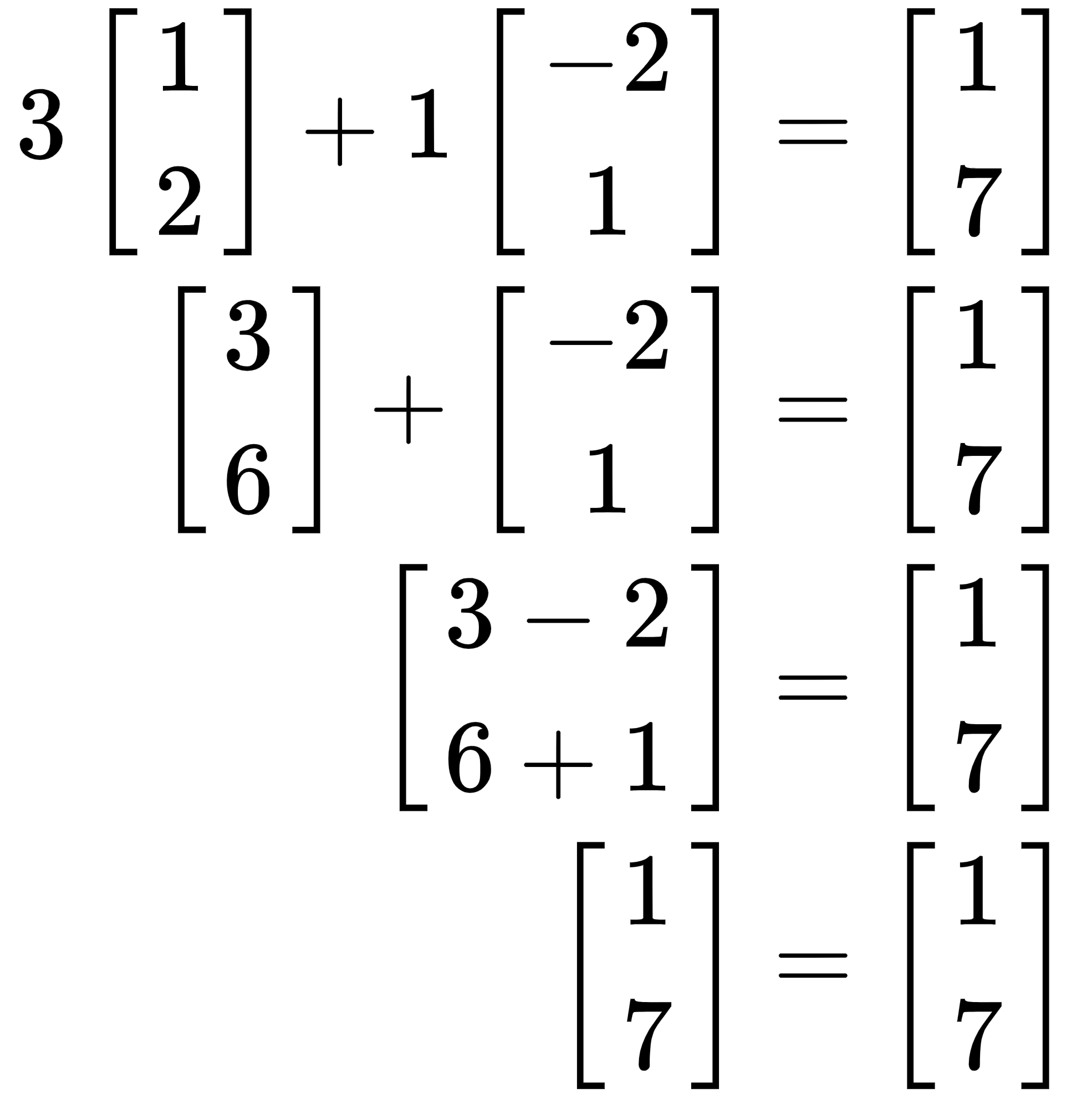
As we can see, the left-hand side is equal to the right-hand side, so it is, in fact, a solution! However, I personally prefer to write this as a coefficient matrix, like so:
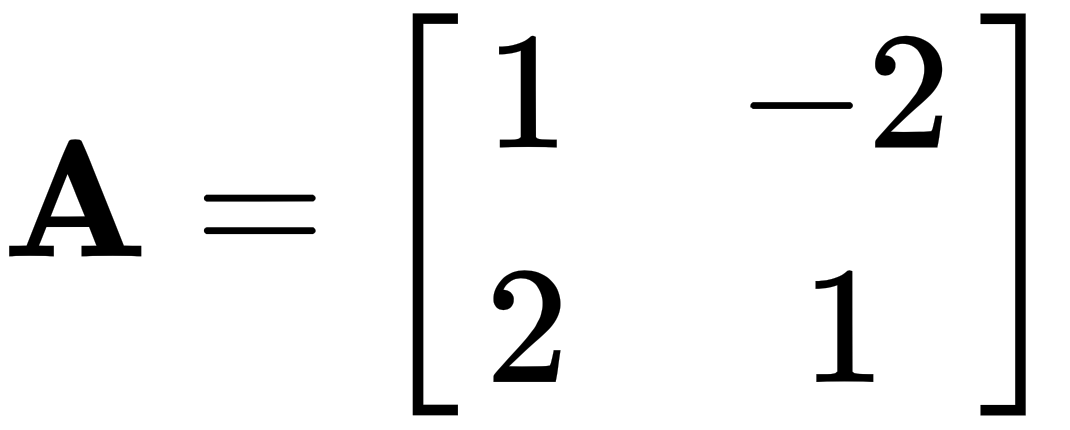
Using the coefficient matrix, we can express the system of equations as a matrix problem in the form  , where the column vector v is the variable vector. We write this as shown:
, where the column vector v is the variable vector. We write this as shown:
 .
.
Going forward, we will express all our problems in this format.
To develop a better understanding, we'll break down the multiplication of matrix A and vector v. It is easiest to think of it as a linear combination of vectors. Let's take a look at the following example with a 3x3 matrix and a 3x1 vector:
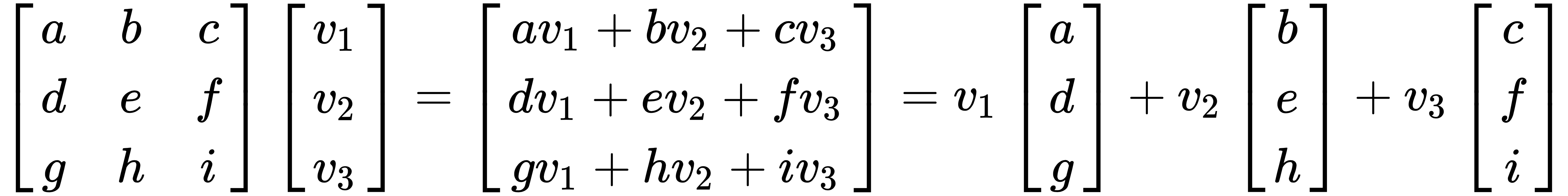
It is important to note that matrix and vector multiplication is only possible when the number of columns in the matrix is equal to the number of rows (elements) in the vector.
For example, let's look at the following matrix:
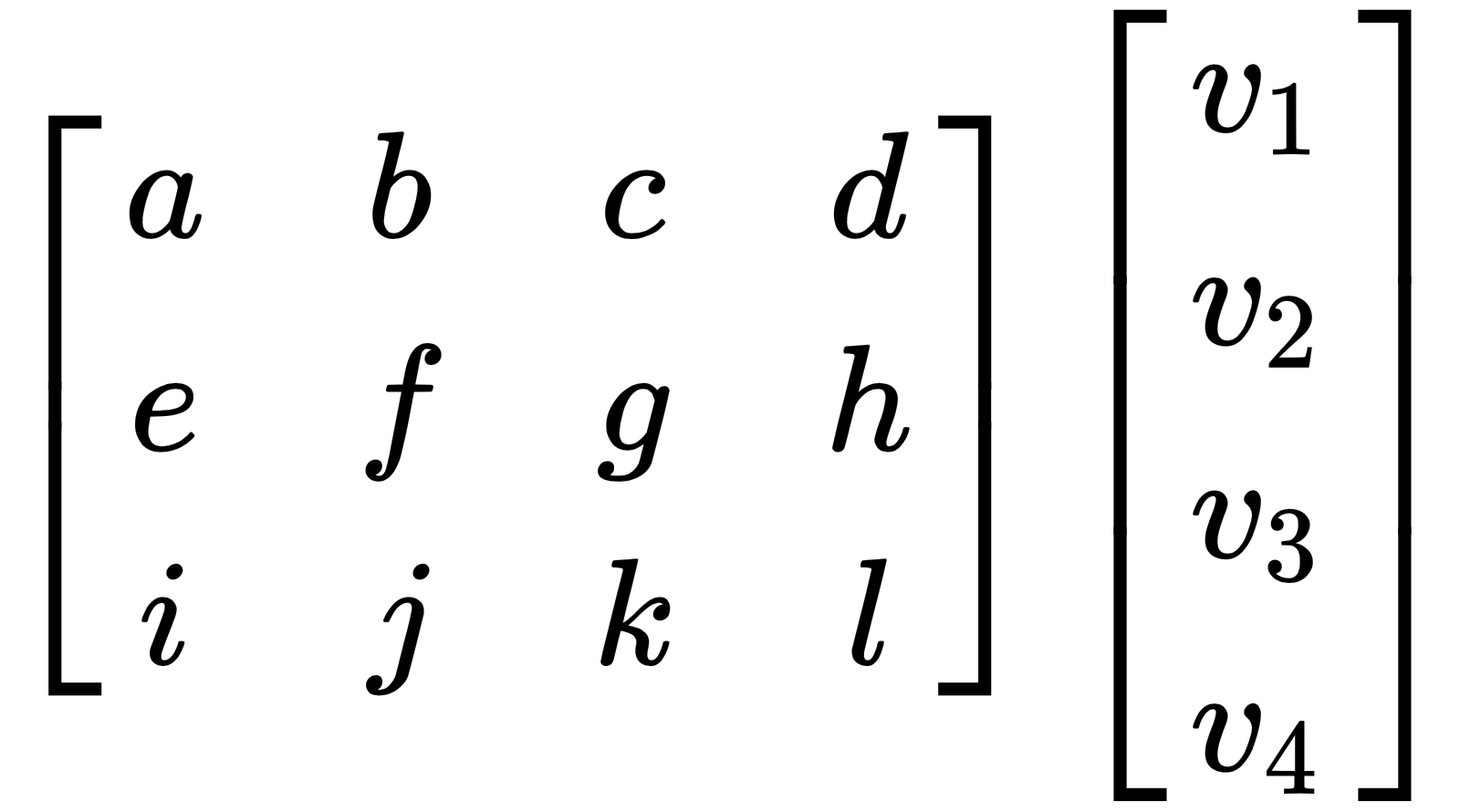
This can be multiplied since the number of columns in the matrix is equal to the number of rows in the vector, but the following matrix cannot be multiplied as the number of columns and number of rows are not equal:
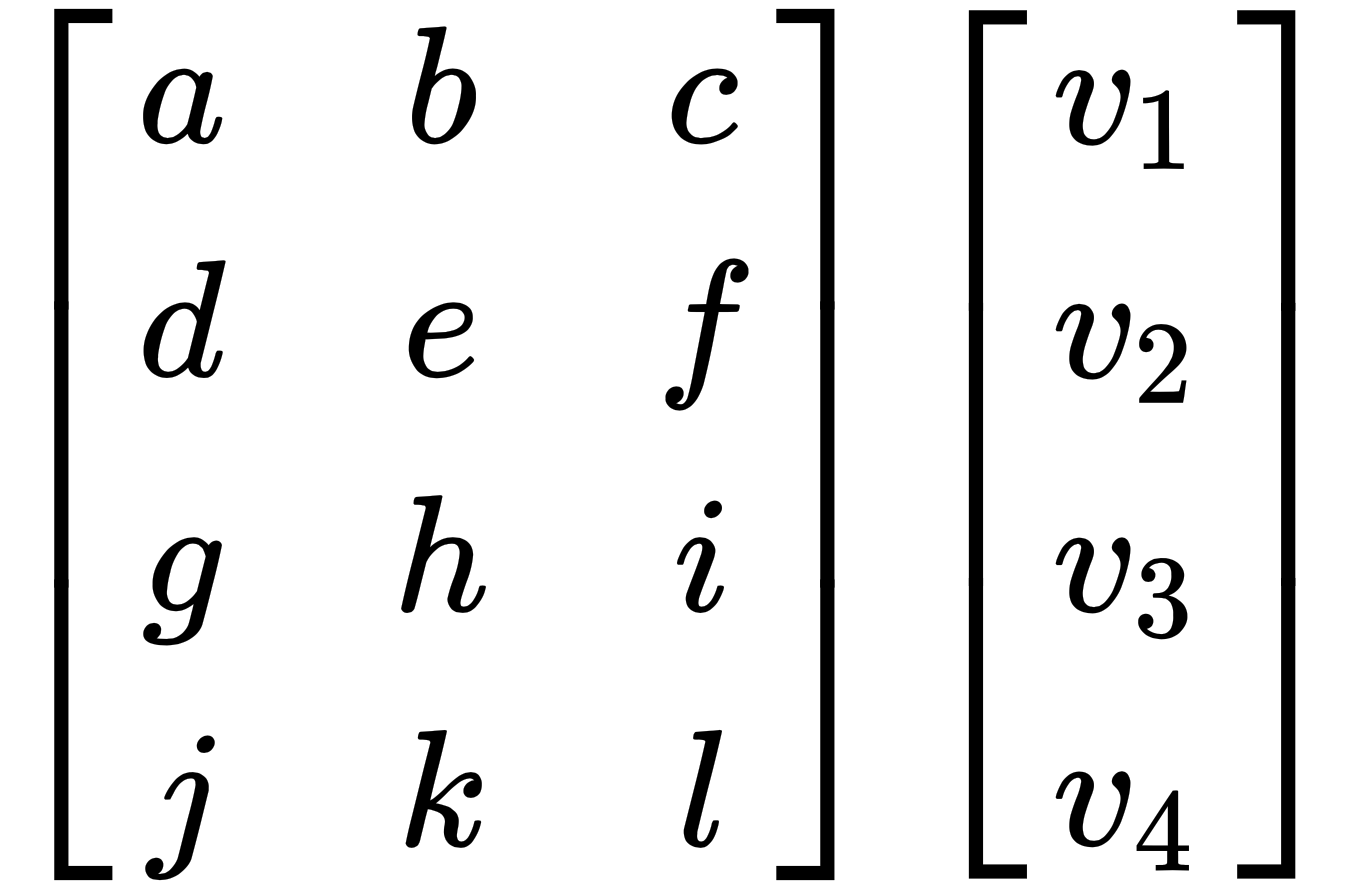
Let's visualize some of the operations on vectors to create an intuition of how they work. Have a look at the following screenshot:
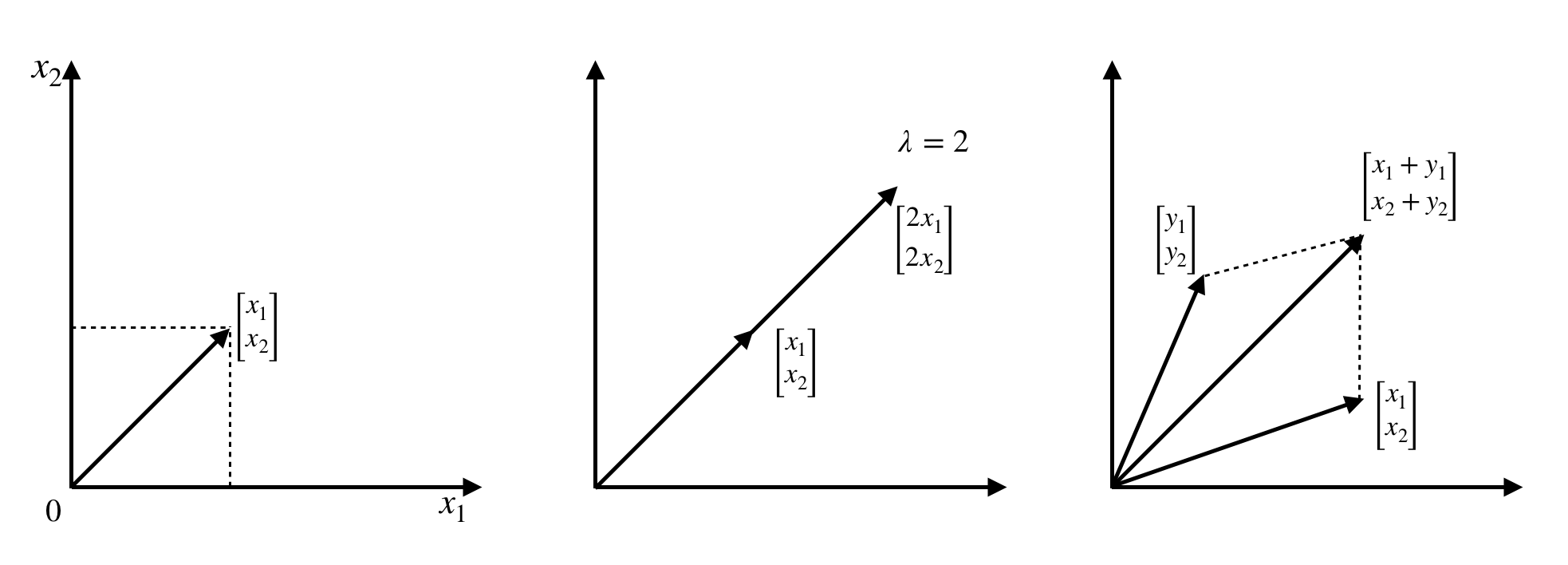
The preceding vectors we dealt with are all in  (in 2-dimensional space), and all resulting combinations of these vectors will also be in
(in 2-dimensional space), and all resulting combinations of these vectors will also be in  . The same applies for vectors in
. The same applies for vectors in  ,
,  , and
, and  .
.
There is another very important vector operation called the dot product, which is a type of multiplication. Let's take two arbitrary vectors in  , v and w, and find its dot product, like this:
, v and w, and find its dot product, like this:
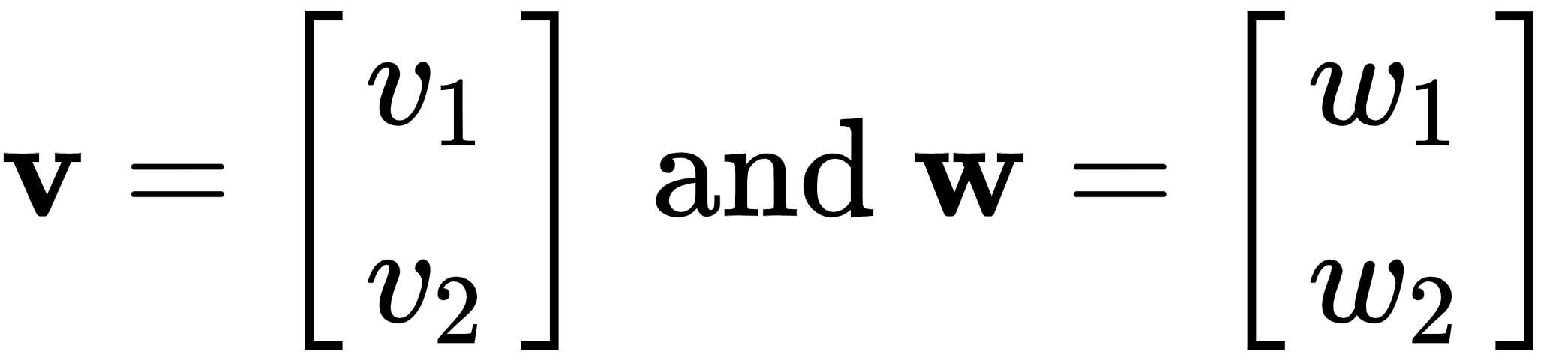
The following is the product:
 .
.
Let's continue, using the same vectors we dealt with before, as follows:
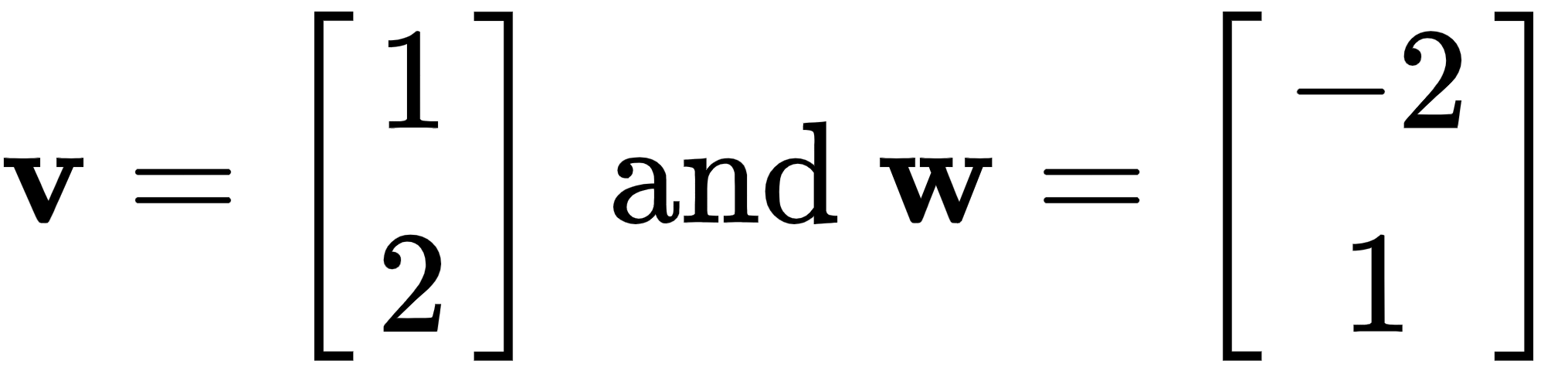
And by taking their dot product, we get zero, which tells us that the two vectors are perpendicular (there is a 90° angle between them), as shown here:

The most common example of a perpendicular vector is seen with the vectors that represent the x axis, the y axis, and so on. In  , we write the x axis vector as
, we write the x axis vector as  and the y axis vector as
and the y axis vector as  . If we take the dot product i•j, we find that it is equal to zero, and they are thus perpendicular.
. If we take the dot product i•j, we find that it is equal to zero, and they are thus perpendicular.
By combining i and j into a 2x2 matrix, we get the following identity matrix, which is a very important matrix:
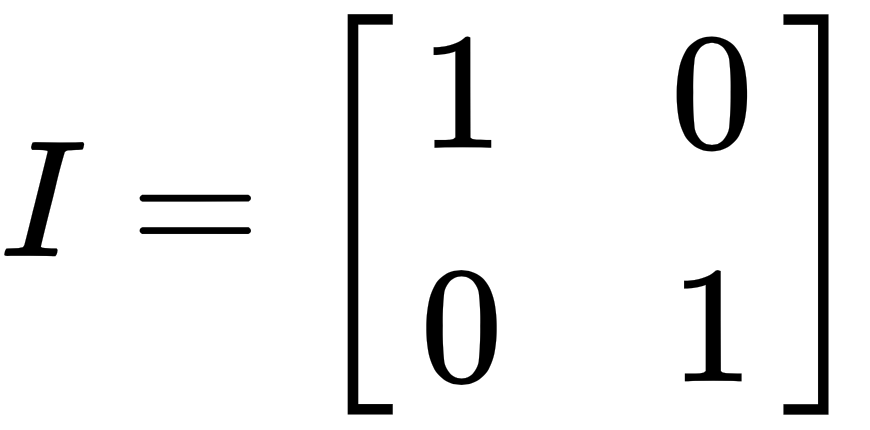
The following are some of the scenarios we will face when solving linear equations of the type  :
:
- Let's consider the matrix
 and the equations
and the equations  and
and  . If we do the algebra and multiply the first equation by 3, we get
. If we do the algebra and multiply the first equation by 3, we get  . But the second equation is equal to zero, which means that these two equations do not intersect and therefore have no solution. When one column is dependent on another—that is, is a multiple of another column—all combinations of
. But the second equation is equal to zero, which means that these two equations do not intersect and therefore have no solution. When one column is dependent on another—that is, is a multiple of another column—all combinations of  and
and  lie in the same direction. However, seeing as
lie in the same direction. However, seeing as  is not a combination of the two aforementioned column vectors and does not lie on the same line, it cannot be a solution to the equation.
is not a combination of the two aforementioned column vectors and does not lie on the same line, it cannot be a solution to the equation. - Let's take the same matrix as before, but this time,
 . Since b is on the line and is a combination of the dependent vectors, there is an infinite number of solutions. We say that b is in the column space of A. While there is only one specific combination of v that produces b, there are infinite combinations of the column vectors that result in the zero vector (0). For example, for any value, a, we have the following:
. Since b is on the line and is a combination of the dependent vectors, there is an infinite number of solutions. We say that b is in the column space of A. While there is only one specific combination of v that produces b, there are infinite combinations of the column vectors that result in the zero vector (0). For example, for any value, a, we have the following:
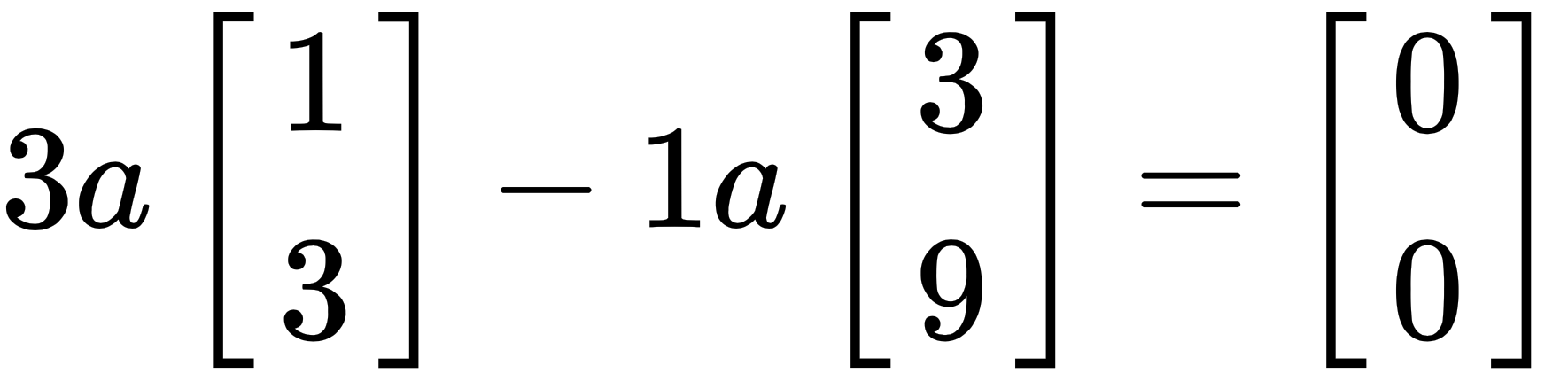
This leads us to another very important concept, known as the complete solution. The complete solution is all the possible ways to produce  . We write this as
. We write this as  , where
, where  .
.
























































 .
. (equation 1) produces a plane, as do
(equation 1) produces a plane, as do  (equation 2), and
(equation 2), and  (equation 3).
(equation 3). , which is the solution to our problem.
, which is the solution to our problem.









 ,
,  , and
, and  .
. becomes
becomes  , as illustrated here:
, as illustrated here:
 , using our found values for x, y, and z, like this:
, using our found values for x, y, and z, like this:



 .
.
 , so that the following applies:
, so that the following applies:

 to the matrix at l3,1 to represent the
to the matrix at l3,1 to represent the  operation, so it becomes the following:
operation, so it becomes the following:

 , which is very valid. The elimination process tends to work quite well, but we have to additionally apply all the operations we did on A to b as well, and this involves extra steps. However, LU factorization is only applied to A.
, which is very valid. The elimination process tends to work quite well, but we have to additionally apply all the operations we did on A to b as well, and this involves extra steps. However, LU factorization is only applied to A. 
 and get the following result:
and get the following result:
 , and we already know from the preceding equation that
, and we already know from the preceding equation that  (so
(so  ). And by using back substitution, we can find the vector v.
). And by using back substitution, we can find the vector v.





















