Drawing a Bezier curve
A Bezier curve is different from a quadratic curve. It is also known as a cubic curve and is the most advanced curvature available in HTML5. The simple Bezier curve looks as shown in the output of this recipe:
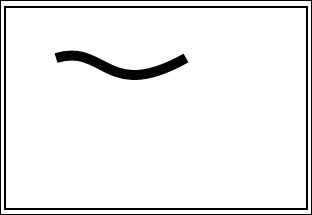
How to do it...
The recipe is as follows:
<html>
<head>
<title>A Bezier Curve</title>
<script>
function init()
{
can = document.getElementById("MyCanvasArea");
ctx = can.getContext("2d");
var xstart = 50; var ystart = 50;
var xctrl1 = 100; var yctrl1 = 35;
var xctrl2 = 100; var yctrl2 = 95;
var xend = 180; var yend = ystart;
//call to the function
drawBezierCurve(xstart,ystart,xctrl1,yctrl1,xctrl2,yctrl2,xend,yend,"black",10);
}
function drawBezierCurve(xstart,ystart,xctrl1,yctrl1,xctrl2,yctrl2,xend,yend,color,width)
{
ctx.strokeStyle=color;
ctx.lineWidth=width;
ctx.beginPath();
ctx.moveTo(xstart,ystart);
ctx.bezierCurveTo(xctrl1,yctrl1,xctrl2,yctrl2,xend,yend);
ctx.stroke();
}
</script>
</head>
<body onload="init()">
<canvas id="MyCanvasArea" width ="300" height="200" style="border:2px solid black">
Your browser doesn't currently support HTML5 Canvas.
</canvas>
</body>
</html>How it works...
In a Bezier curve there are two control points, one start point and one end point. So you have to move to the starting or context point, like we do in a quadratic curve, and then specify the control points and ending point in the bezierCurveTo(cp1X,cp1Y,cp2X,cp2Y,epX,epY) method. Here, cp1 and cp2 are the control points and ep is the end point. The two control points add more flexibility to the curve.
Refer to the diagram given here:
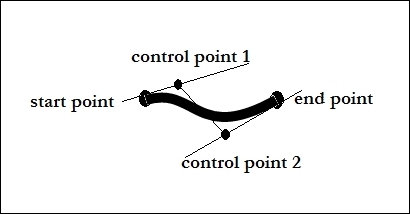
The curve starts at the start/context point and ends at the end point. It heads towards control point 1 and then comes down to the end point through control point 2. The control points control the curvature. Change the y coordinate of any control point and you will see the difference.
Bezier curves are actually a sequence of cubic segments rather than linear segments. They appear smooth at all scales and are used in computer graphics.




























































