Similarity measures
A similarity measure is like an inverse distance function. In fact, if d(y, z) is a distance function on the set of all items, we could use this:
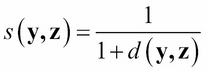
as a similarity measure. You can check that this would satisfy the six properties for a similarity measure, enumerated previously.
Without a predefined distance function to use, we instead will want to define the similarity measure in terms of the contents of the given utility matrix. There are several ways to do this.
If the utility matrix is Boolean (that is, every entry uij is either 1 or 0, indicating whether user i has bought an item), then we could adapt the Hamming metric. In this case, each column of the utility matrix is a Boolean vector, indicating which users have bought that item. The Hamming distance between two Boolean vectors is the number of vector slots where they differ. For example, if y = (1, 1, 1, 0, 0, 1, 0, 0) and z = (1, 0, 1, 1, 1, 0, 0, 1), then the Hamming distance between y and z is dH(y, z) = 5, because...



































































