We all love programs! On one side, there are surgical programming languages such as C and C++, which can solve the problem with clinical efficiency. This can be good and bad at the same time. A very experienced programmer can write a very efficient code; at the same time, it is also possible to write code that is unintelligible and very difficult to understand. On the other side, there are programs that are elegant, composable, and not only easier to understand, but also easier to reason with, such as Lisp, ML, and Haskell.
It is the second kind of programs that we will be looking at in this book. Not that efficiency is not important to us, nor does it mean that we cannot write elegant programs in C/C++. However, we will concentrate more on expressiveness, modularity, and composability of the programs. We will be interested more on the what of the program and not really on the how of the program.
Understanding the difference between what and how is very critical to understand the expressiveness, composability, and reasoning power of functional languages. Working with functional languages involves working with expressions and evaluations of expressions. The programmer builds functions consisting of expressions and composes them together to solve a problem at hand. Essentially, a functional programmer is working towards construction of a function to solve the problem that they are working on.
We will look at a program written in Haskell. The program adds two integers and returns the result of addition as follows:
add :: Int -> Int -> Int
add a b = a + b
Here, the add function takes two arguments, which are applied to the expression on the right-hand side. Hence, the expression add a b is equivalent to a + b. Unlike programming languages such as C/C++, add a b is not an instruction, but expressions and application of the values a and b to the expression on the right-hand side and the value of the expression. In short, one can say that add a b is bound to value of the expression a + b. When we call add 10 20, the expression is applied to the values 10 and 20, respectively. In this way, the add function is equivalent to a value that evaluates to an expression to which two values can be applied.
The functional program is free to evaluate the expression in multiple ways. One possible execution in a functional context is shown in the following diagram. You can see that add a b is an expression with two variables a and b as follows:
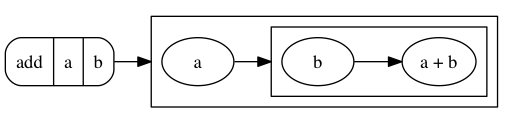
When value 10 is bound to variable b, the expression substitutes the value of b in the expression on the right-hand side:

Now, the whole expression is reduced to an expression in a:
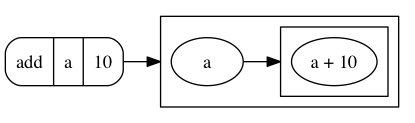
When value 20 is bound to variable a, the expression again substitutes the value of a in the expression on the right-hand side:
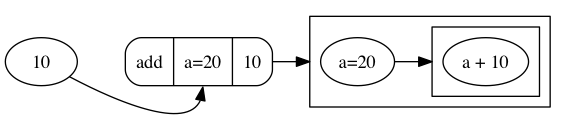
Finally, the expression is reduced to a simple expression:
Note that in the expression add a b, a and b can both be expressions. We can either evaluate the expressions before substitution, or we can substitute the expressions first and then reduce them. For example, an expression add (add 10 20) 30 can be substituted in the expression a + b as follows:
add (add 10 20) 30 = (10 + 20) + 30
Alternatively, it can be substituted by evaluating add 10 20 first and then substituting in the expression as follows:
add (add 10 20) 30 = add (10 + 20) 30
= add 30 30
= 30 + 30
The first approach is called call by name, and the second approach is called call by value. Whichever approach we take, the value of the expression remains the same. In practice, languages such as Haskell take an intelligent approach, which is more geared towards efficiency. In Haskell, expressions are typically reduced to weak-headed normal form in which not the whole expression is evaluated, but rather a selective reduction is carried out and then is substituted in the expression.


































































