Now, we have a defined loss metric, which computes the error between the optimal Q-function (derived from the Bellman equation) and the current Q-function at a given time. We can then propagate our prediction errors in Q-values, backwards through the model layers, as our network plays about the environment. As we are well aware of by now, this is achieved by taking the gradient of the loss function with respect to model weights, and then updating these weights in the opposite direction of the gradient per learning batch. Hence, we can iteratively update the model weights in the direction of the optimal Q-value function. We can formulate the backpropagation process and illustrate the change in model weights (theta) like so:
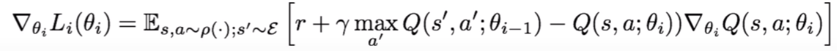
Eventually, as the model has seen enough state action pairs, it will sufficiently backpropagate its errors and learn...



























































