Superposition
Superposition can be a very imposing term, so before we delve into it, let's take a step back and talk about the computers we use today. In quantum computing, we call these computers "classical computers" to distinguish them from quantum computers. Classical computers use binary digits—or bits, for short—to store ones and zeros. These ones and zeros can represent anything, from truth values to characters to pixel values on a screen! They are physically implemented using any two-state device such as an electrical switch that is either on or off.
A quantum bit, or qubit for short, is the analogous building block of quantum computers. They are implemented by anything that demonstrates quantum phenomena, which means they are very, very small. In the following screenshot, we show how a property of an electron—namely spin—can be used to represent a one or zero of a qubit:
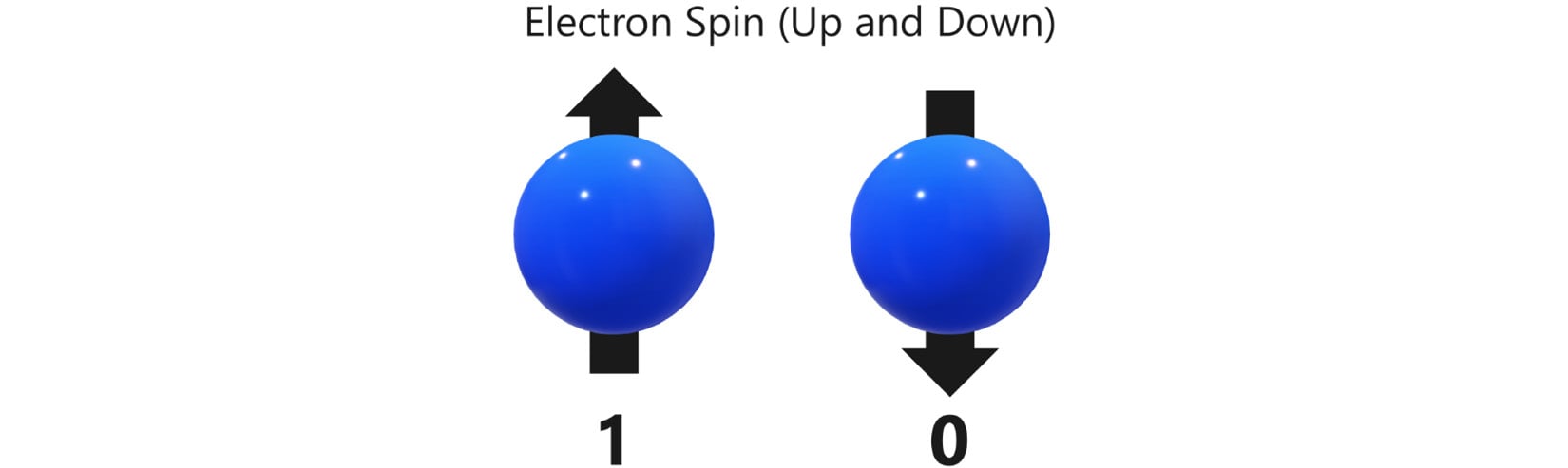
Figure 1.9 – Pair of electrons with a spin labeled 1 and 0
Physicists use mathematics to model quantum phenomena, and guess what they use to model the state of a quantum particle? That's right! Vectors! Quantum computer scientists have taken two of these states and labeled them as the canonical one and zero for qubits. They are shown in the following screenshot:
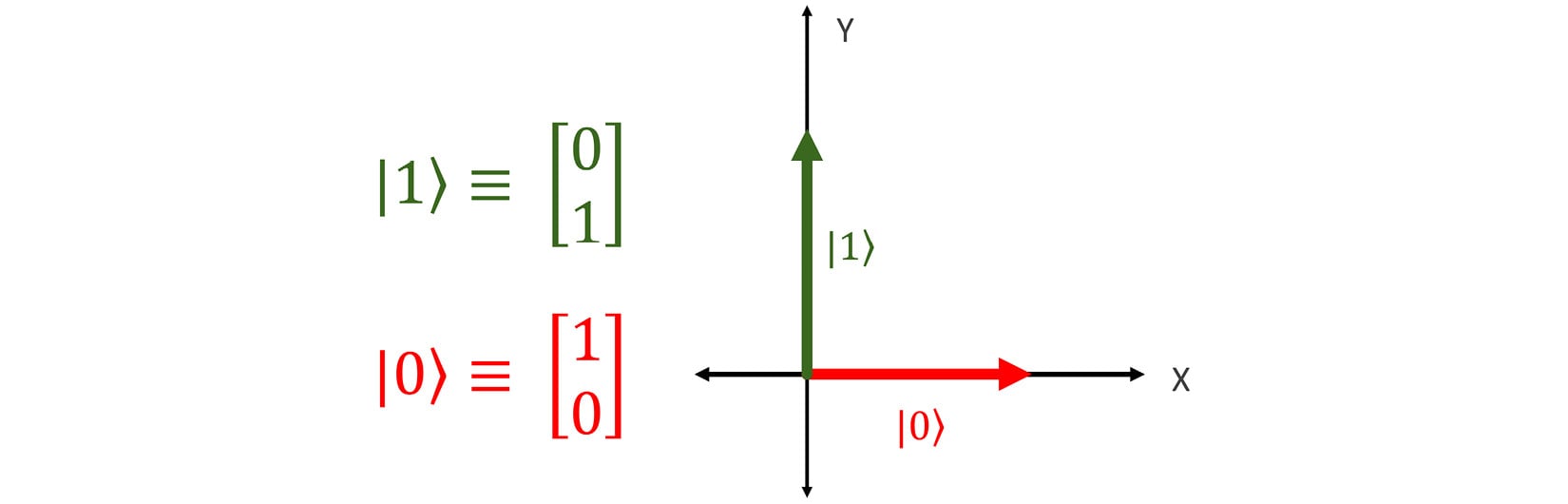
Figure 1.10 – Zero and one states
As you can see, the zero and one states are just vectors on the x and y axes with a length of one unit each. When you combine a lot of ones and zeros in classical computing, wonderful, complex things can be done. The same is true of the zero and one state of qubits in quantum computing.
Greek Letters
Mathematicians and physicists love Greek letters, and they have found their way into quantum computing in several places. The Greek letter "Psi", ψ, is often used to represent the state of a qubit. The Greek letters "alpha", α, and "beta", β, are used to represent numbers or scalars.
While qubits can represent a one or a zero, they have a superpower in that they can represent a combination of a zero and one as well! "How?" you might ask. Well, this is where superposition comes in. Understanding it is actually quite simple from a mathematical standpoint. In fact, you already know what it is! It's just a fancy way of saying that a qubit is in a linear combination of states.
If you recall, we defined the vector |e⟩ as a linear combination of the aforementioned |a⟩ and |b⟩, like so:
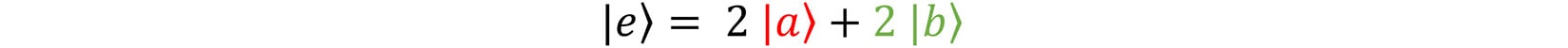
Figure 1.11 – Definition of |e⟩
If we replace those letters and numbers with the Greek letters and the zero and one states we just introduced, we get an equation like this:
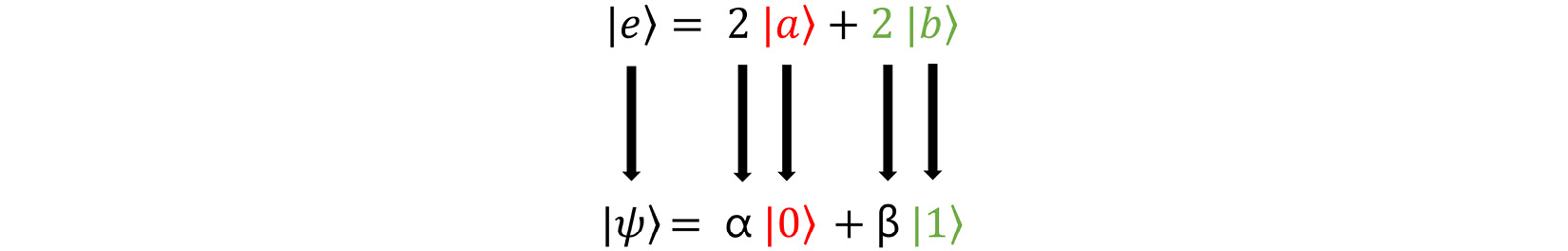
Figure 1.12 – Greek letters being transposed onto a linear combination equation
The bottom equation represents a qubit in the state |ψ⟩, which is a superposition of the states zero and one! You now know what superposition is mathematically! This, by the way, is the only way that counts because math is the language of physics and, therefore, quantum computing.
Measurement
But wait—there's more! With only the simple mathematics you have acquired so far, you also get a look at the weird act of measuring qubits. The scalars α and β shown previously play a crucial role when measuring qubits. In fact, if we were to set this qubit up in the state |ψ⟩ an infinite number of times, when we measured it for a zero or a one, |α|2 would give us the probability of getting a zero, and |β|2 would give us the probability of getting a one. Pretty cool, eh!?!
So, here is a question. For the qubit state |ψ⟩ in the following equation, what is the probability of getting a zero or a one when we measure it?

Well, if we said |α|2 gives us the probability of getting a zero, then the answer would look like this:

This tells us that one half or 50% of the time when we measure for a zero or a one, we will get a zero. We can do the same exact math for β and derive that the other half of the time when we measure, we will get a one. The state |ψ⟩ shown previously represents the proverbial coin being flipped into the air and landing heads for a one and tails for a zero.

































































