Recursive functions
In mathematics, many functions are defined recursively. In this section, we will show how this concept can be used even when programming a function. This makes the relation of the program to its mathematical counterpart very clear, which may ease the readability of the program.
Nevertheless, we recommend that you use this programming technique with care, especially within scientific computing. In most applications, the more straightforward iterative approach is more efficient. This will become immediately clear from the following example.
Chebyshev polynomials are defined by a three-term recursion:
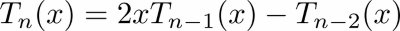
Such a recursion needs to be initialized, that is, T0(x) =1, T1(x) = x.
In Python, this three term recursion can be realized by the following function definition:
def chebyshev(n, x): if n == 0: return 1. elif n == 1: return x else: return 2. * x * chebyshev(n - 1, x) - chebyshev(n...























































