The hidden Markov model (HMM)
A HMM is indeed a Markov process (also known as a Markov chain) for observations with a discrete time. The main difference with the Markov processes is that the states are not observable. A new observation is emitted with a probability known as the emission probability, each time the state of the system or model changes.
There are now two sources of randomness:
Transition between states
Emission of an observation when a state is given
Let's reuse the boxes and balls example. If the boxes are hidden states (non-observable), then the user draws the balls whose color is not visible. The emission probability is the probability bik =p(ot = colork | qt =Si) to retrieve a ball of the color k from a hidden box I, as described in the following diagram:
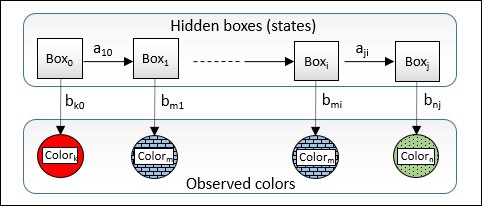
The HMM for the balls and boxes example
In this example, we do not assume that all the boxes contain balls of different colors. We cannot make any assumptions on the order as defined by the transition aij. The HMM does not...









































































