In this section, you will learn how to solve linear equations by using the linalg.solve() method. When you have a linear equation to solve, as in the form  , in simple cases you can just calculate the inverse of A and then multiply it by B to get the solution, but when A has a high dimensionality, that makes it very hard computationally to calculate the inverse of A. Let's start with an example of three linear equations with three unknowns, as follows:
, in simple cases you can just calculate the inverse of A and then multiply it by B to get the solution, but when A has a high dimensionality, that makes it very hard computationally to calculate the inverse of A. Let's start with an example of three linear equations with three unknowns, as follows:

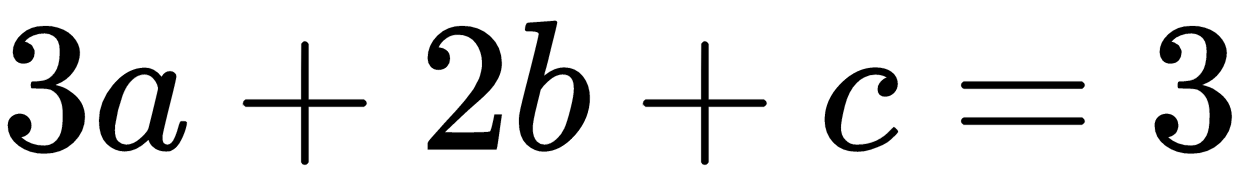
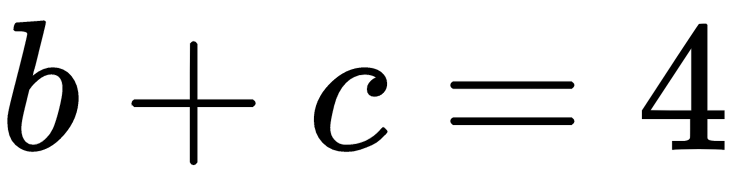
So, these equations can be formalized as follows with matrices:
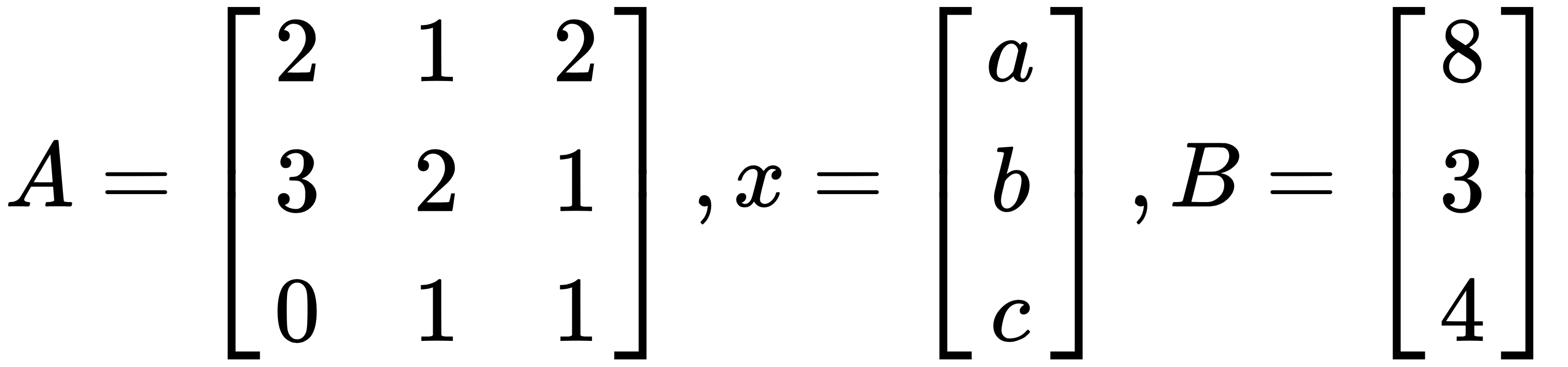
Then, our problem is to solve  . We can calculate the solution with a plain vanilla NumPy without using linalg.solve(). After inverting the A matrix, you will multiply with B in order to get results for x. In the following code block, we calculate the dot product for the inverse matrix of A and B in order to calculate
. We can calculate the solution with a plain vanilla NumPy without using linalg.solve(). After inverting the A matrix, you will multiply with B in order to get results for x. In the following code block, we calculate the dot product for the inverse matrix of A and B in order to calculate  :
:
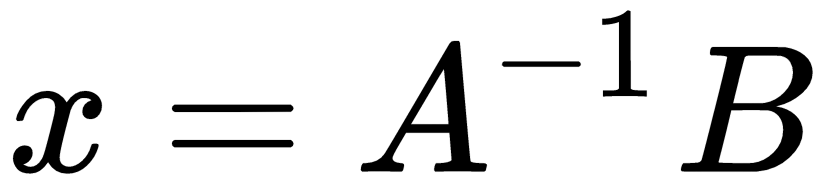
In [44]: A =...












































































