Amazon ML is based on linear modeling. Recall the equation for a straight line in the plan:
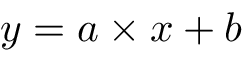
This linear equation with coefficients (a, b) can be interpreted as a predictive linear model with x as the predictor and y as the outcome. In this simple case, we have two parameters (a, b) and one predictor x. An example can be that of predicting the height of children with respect to their weight and find some a and b such that the following equation is true:
Let's consider the classic Lewis Taylor (1967) dataset with 237 samples of children's age, weight, height, and gender (https://v8doc.sas.com/sashtml/stat/chap55/sect51.htm) and focus on the relation between the height and weight of the children. In this dataset, the optimal regression line follows the following equation:
The following figure illustrates the height versus weight dataset and the associated linear regression:
Consider now that we have not one predictor but several, and let's generalize the preceding linear equation to N predictors denoted by {x1, . . . , xn} and N +1 coefficients or {wo, w1, . . ., wn} weights. The linear model can be written as follows:
Here, ŷ denotes the predicted value, (y would correspond to the true value to be predicted). To simplify notations, we will assume for the rest of the book the coefficient wo = 0.
This equation can be rewritten in vector form as follows:
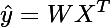
Where T is the transpose operator, X = {x1, . . ., xn} and W= {w1, . . .,wn} are the respective vectors of predictors and model weights. Under certain conditions, the coefficients wi can be calculated precisely. However, for a large number of samples N, these calculations are expensive in terms of required computations as they involve inverting matrices of dimension N, which for large datasets is costly and slow. As the number of samples grows, it becomes more efficient to estimate these model coefficients via an iterative process.
The Stochastic Gradient Descent algorithm iteratively estimates the coefficients {wo, w1, . . ., wn} of the model. At each iteration, it uses a random sample of the training dataset for which the real outcome value is known. The SGD algorithm works by minimizing a function of the prediction error:
Functions that take the prediction error as argument are also called loss functions. Different loss functions result in different algorithms. A convex loss function has a unique minimum, which corresponds to the optimal set of weights for the regression problem. We will come back to the SGD algorithm in details in later chapters. Suffice to say for now that the SGD algorithm is especially well-suited to deal with large datasets.
There are many reasons to justify selecting the SGD algorithm for general purpose predictive analysis problems:
- It is robust
- Its convergence properties have been extensively studied and are well known
- It is well adapted to optimization techniques
- It has many extensions and variants
- It has low computational cost
- It can be applied to regression, classification, and streaming data
Some weaknesses include the following:
- The need to properly initialize its parameters
- A convergence rate dependent on a parameter called the learning rate
 United States
United States
 United Kingdom
United Kingdom
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Argentina
Argentina
 Austria
Austria
 Belgium
Belgium
 Bulgaria
Bulgaria
 Chile
Chile
 Colombia
Colombia
 Cyprus
Cyprus
 Czechia
Czechia
 Denmark
Denmark
 Ecuador
Ecuador
 Egypt
Egypt
 Estonia
Estonia
 Finland
Finland
 Greece
Greece
 Hungary
Hungary
 Indonesia
Indonesia
 Ireland
Ireland
 Italy
Italy
 Japan
Japan
 Latvia
Latvia
 Lithuania
Lithuania
 Luxembourg
Luxembourg
 Malaysia
Malaysia
 Malta
Malta
 Mexico
Mexico
 Netherlands
Netherlands
 New Zealand
New Zealand
 Norway
Norway
 Philippines
Philippines
 Poland
Poland
 Portugal
Portugal
 Romania
Romania
 Singapore
Singapore
 Slovakia
Slovakia
 Slovenia
Slovenia
 South Africa
South Africa
 South Korea
South Korea
 Sweden
Sweden
 Switzerland
Switzerland
 Taiwan
Taiwan
 Thailand
Thailand
 Turkey
Turkey
 Ukraine
Ukraine










![Microsoft Power BI - The Complete Masterclass [2023 EDITION]](https://content.packt.com/V19592/cover_image.jpg)






