What is an ASIC?
ASICs are the fundamental building blocks of modern electronics – your laptop or PC, TV, cell phone, digital watch, almost everything you use on a day-to-day basis. It is also the fundamental building block upon which the FPGA we will be looking at is built. In short, an ASIC is a custom-built chip designed using the same language and methods we will be introducing in this book.
Note: This section is for reference and an introduction to basic digital electronics. ASICs and FPGAs are both developed using similar Hardware Descriptive Language (HDL) coding methods. This opens up additional career opportunities for someone with this knowledge.
FPGAs came about as the technology to create ASICs followed Moore’s law (Gordon E. Moore, Cramming More Components Onto Integrated Circuits, Electronics, Volume 38, Number 8, https://archive.computerhistory.org/resources/access/text/2017/03/102770822-05-01-acc.pdf) – the idea that the number of transistors on a chip doubles every 2 years. This has both allowed for very cheap electronics, in the case of mass-produced items containing ASICs, and led to the proliferation of lower-cost FPGAs.
The first commercial FPGA was introduced by Xilinx in 1985, the XC2064. This part is only slightly larger than the Combination Logic Block (CLB)s we’ll look at later, but at the time, it was revolutionary. Prior to this, the only programmable logic was based on Erasable Programmable Memory (EPROM) arrays to implement small logic functions, sometimes with storage elements included on the chip. This was long before HDL languages were used to program the devices and they were often configured with a much simpler syntaxed language.
FPGAs are an ASIC at heart. Xilinx has used an ASIC process to create a reconfigurable chip. However, we must consider the trade-offs in choosing an FPGA or ASIC.
Why an ASIC or FPGA?
ASICs can be an inexpensive part when manufactured in high volumes. You can buy a disposable calculator, a flash drive for pennies/cents per gigabyte, or an inexpensive cell phone; they are all powered by at least one ASIC. ASICs are also sometimes a necessity when speed is of the utmost importance, or the amount of logic that is needed is very large. However, in these cases, they are typically only used when cost is not a factor.
We can break down the costs of developing a product based on an ASIC or FPGA into Non-Recurring Engineering (NRE), the one-time cost to develop a chip, and the piece price for every chip, excluding NRE. Ed Sperling stated the following in CEO Outlook: It Gets Much Harder From Here, Semiconductor Engineering, June 3, 2019, https://semiengineering.com/ceo-outlook-the-easy-stuff-is-over/: “The NRE for a 7nm chip is $25 million to $30 million, including mask set and labor.”
These costs are a necessity to build a chip and the main reason why ASICs, especially very advanced ones, are very expensive to produce. They include more than just the mask sets, the blueprint for the ASIC, if you will, that is used to deposit the materials on the silicon wafers that build the chip. These costs also include the salaries for teams of design, implementation, and verification engineers that can number into the hundreds. Re-spins, or bug fixes, are usually factored into ASIC costs because large, complex devices struggle with first-time success.
Compare this to an FPGA, where complex chips can be developed by a single person or small teams. Most of the NRE has been shouldered by the FPGA vendor in the design of the FPGA chips, which are known good quantities. The little NRE expense left is for tools and engineering. Re-spins are free, except for time, since the chip can be reprogrammed using flash memory, without million-dollar mask sets.
The trade-off is the per-part cost. High-volume ASICs with low complexity, like the one inside a pocket calculator or a digital watch, can cost pennies. CPUs can run into the hundreds or thousands of dollars. Compare that to FPGAs where even the most inexpensive Spartan-7 starts at a few dollars, and the largest and fastest can stretch into tens of thousands of dollars.
Another factor is tool costs. As we will see in Chapter 2, FPGA Programming Languages and Tools, AMD provides the Xilinx Vivado tool suite for free for the smaller parts. Other FPGA vendors, such as Intel (formerly Altera), also offer free versions for lower-end parts. This speeds up adoption, where the barrier to entry is now a computer and a development board. Even the cost of developing more expensive parts is only a few thousand dollars if you need to purchase a professional copy of Vivado for AMD or Quartus for Intel. In contrast, ASIC tools can run into millions of dollars and require years of training since the risk of failure is extremely high. As we will see in our projects, we’ll make mistakes, sometimes to demonstrate a concept, but the cost to fix it will only be a few minutes, mostly spent on understanding why it actually failed.
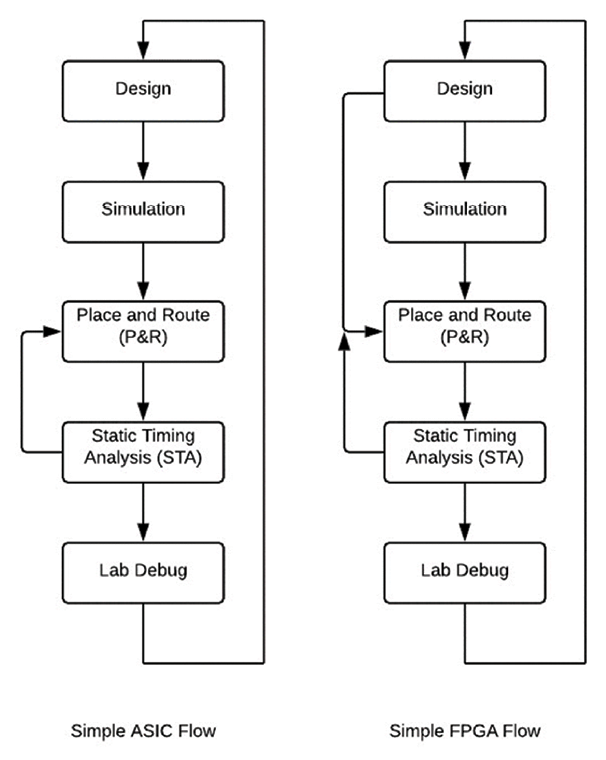
Figure 1.1: Simple ASIC versus FPGA flow
The flow for an ASIC or FPGA is essentially the same as shown above in Figure 1.1. ASIC flows tend to be more linear in that you have one chance to make a working part. With an FPGA, things such as simulation can become an option, although strongly suggested for complex designs. One difference is that the lab debug stage can also act as a form of simulation by using ChipScope, or similar on-chip debugging techniques, to monitor internal signals for debugging. The main difference is that each iteration through the steps costs only time in an FPGA flow. In this situation, any changes to a fabricated ASIC design would require some number of new mask sets, the costs of which could run into the millions of dollars.
We summarize the choice between an ASIC and FPGA in Table 1.1 below:
|
FPGA |
ASIC |
|
Mostly reprogrammable |
Limited or no programmability |
|
Very high piece price |
Extremely low to high piece price, usually based on volumes |
|
Very low NRE |
Very high NRE |
|
Low tool cost |
Very high tool cost |
|
Easy to debug in lab/high visibility into design |
Usually limited ability to view internal states |
Table 1.1: FPGA versus ASIC summary
We’ve briefly looked at what an ASIC is and why we might choose an ASIC or an FPGA for a given application. Now, let’s look at how an FPGA is created using an ASIC process.
How does a company create a programmable device using an ASIC process?
The basis of any ASIC technology is the transistor, with the largest devices made up of billions of transistors. Multiple ASIC processes have been developed over the years, and they all rely on transistors, which can be on or off, represented as 1s and 0s. These can be thought of as Booleans, true or false values.
The basis of Boolean algebra was developed by George Bool in 1847. The fundamentals of Boolean algebra make up the basis of the logic gates upon which all digital logic is formed. The code that we will be writing is at a high level of abstraction from the actual hardware implementation and the tools will convert our design into a physical implementation. It is important to understand the basics and will give us a good springboard for a first project. Thousands of engineers have struggled to build efficient logic by hand in the past using individual ICs on a breadboard. I want to get you past that with a minimum of fuss since modern tools are very good at what they do.
An FPGA company, such as AMD or Intel, develops an FPGA by creating configurable structures that can be loaded at the initialization of the device or modified during runtime. The same techniques we will talk about here are used to design blocks that are then synthesized directly into transistors rather than mapped to lookup tables and routing resources. The interesting thing about the fact that the same design techniques are used for FPGAs and ASICs is that many ASICs are prototyped on FPGAs to minimize logic errors and re-spins.
We’ll need to know a little Hardware Description Language (HDL) such as Very High Speed Integrated Circuit HDL (VHDL) or SystemVerilog to go through this section.
Introduction to HDLs
We’ll need to define some terminology for discussing HDLs.
Logical versus bitwise operations
Logical functions operate on Boolean values. A Boolean is an object that can hold one of two values: true or false for VHDL, and 1 or 0 for SystemVerilog/Verilog. SystemVerilog/Verilog has no concept of true and false. Note that this can be viewed as an advantage of SystemVerilog as it behaves like hardware in that there is no difference between a 1 and true or 0 and false when you implement hardware. VHDL proponents view the strong typing of VHDL as an important feature since it clarifies intent by forcing the correct types to be used.
A bitwise function operates on a 1 or 0 (or as we will discuss later in the book, other values representing unknown, tri-state or different drive strengths). Both VHDL and SystemVerilog/Verilog have objects that hold these values and are operated on in a bitwise function. We will dive deeper into this in Chapter 3, Combinational Logic, but we’ll be using if statements in some of the examples below to demonstrate the logic gates.
Bitwise functions also have the ability to act as reduction operators in SystemVerilog/Verilog and there are similar functions in VHDL. These will be discussed in Chapter 2, FPGA Programming Languages and Tools.
In this section, we are primarily discussing logical functions. In SystemVerilog and Verilog, logical and bitwise functions can be intermixed as they are weakly typed languages. VHDL is strongly typed and you will run into problems mixing them up. This will be discussed further in Chapter 3.
Armed with this knowledge, let’s dip our toes into some HDL code.
Creating gates using HDL
In this section, we’ll take a look at some basic HDL code that will allow us to demonstrate the gates that underlie all digital designs. We need a way of inferring these operations and we’ll start by looking at signal assignments.
Assign statement (SystemVerilog/Verilog)
We can use an assign statement to take whatever value is on the right-hand side (RHS) of the equal sign to the left-hand side (LHS). Its usage is as follows:
assign out = in;
in can be another signal, function, or operation on multiple signals. out can be any valid signal declared prior to the assign statement. The above code simply acts like a wire.
Assign statement equivalent (VHDL)
In VHDL, a signal can be assigned as follows:
output <= input;
Similar to SystemVerilog/Verilog, whatever is on the RHS will be assigned to the LHS.
in and out are reserved words used for port directions in VHDL. input and output are reserved words used for port direction in SystemVerilog, hence the signal name changes between language examples.
Single line comments
SystemVerilog and VHDL both provide a method for creating a comment on a single line. The comment runs from the comment character, which is // for SystemVerilog or – for VHDL, until the end of the line:
// Everything here is a comment. (SystemVerilog)
-- Everything here is a comment. (VHDL)
Multiline comments
Both SystemVerilog and Verilog share the same type of multiline comments, based upon the C style of comment. Block comments have also been supported in VHDL since 2008:
/*
I can span Multiple Lines
*/
Prior to VHDL-2008, VHDL only supported single line comments (–).
if statement
Both SystemVerilog/Verilog and VHDL provide a way of testing conditions via the if statement. The basic syntax is as follows:
if (condition) …; // SystemVerilog/ Verilog
if condition then ... end if; // VHDL
The if statement will be used throughout the book and there are some nuances that we will discuss in more detail in Chapter 3, Combinational Logic.
With the terminology out of the way, let’s look at Boolean logic gates used Boolean operations.
Fundamental logic gates
There are four basic logic gates. These gates are necessary for anything from simple control logic to complex arithemetic and processing algorithms. AI is all the rage at the time of authoring this book and the heart of every AI system boils down to these simple structures.
We typically write the truth tables for the gates to understand their functionality. A truth table shows us what the output is for every set of inputs to a circuit. Refer to the following example involving a NOT gate.
Logical NOT
The output of the NOT gate produces the opposite value of a signal going in. It’s often called an inverter since it inverts the value. The function in SystemVerilog can be written as follows:
assign out = !in; // logical NOT Boolean operator
In VHDL, we would write:
out <= not in; // Boolean operator
The associated truth table is as follows:
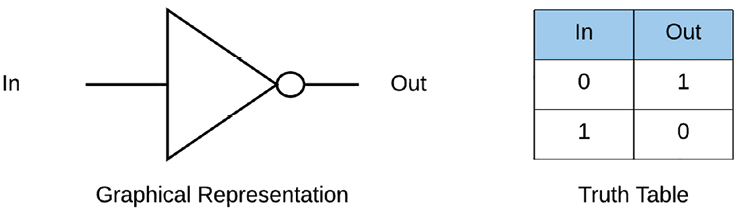
Figure 1.2: NOT gate representation
The NOT gate is one of the most common operators we will be using:
if (!empty) ... // SystemVerilog/Verilog
if not empty then .– -- VHDL
Often, we need to test a signal before performing an operation. For example, if we are using a First In, First Out (FIFO) storage to smooth out sporadic data or for crossing clock domains, we’ll need to test whether there is data available before popping it out for use. FIFOs have flags used for flow control, the two most common being full and empty. We can do this by testing the empty flag, as shown here.
We will go into greater depth in later chapters on how to design a FIFO as well as use one.
Logical AND
Often, we will want to test whether one or more conditions are active at the same time. To do this, we will be using the AND gate. An AND gate tests two or more inputs to determine if all of them are set. If any input is a 0, the AND gate will return a 0. If all of them are set, it will return a 1.
The function in SystemVerilog/Verilog can be written as follows:
assign out = in1 && in0; // logical AND Boolean operator
The function in VHDL can be written as follows:
out <= in1 and in0; -- logical AND Boolean operator
The associated truth table is as follows:
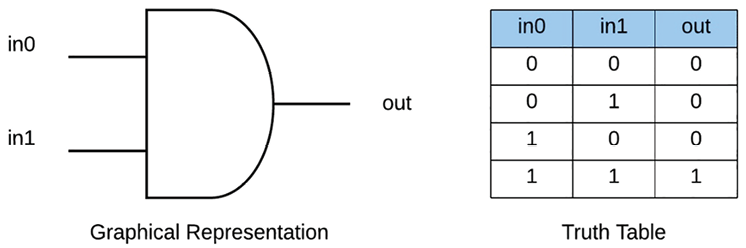
Figure 1.3: AND gate representation
Continuing our FIFO example, you might be popping from one FIFO and pushing into another:
if (!src_fifo_empty && !dst_fifo_full) ... // SV/ Verilog
if (not src_fifo_empty) and (not dst_fifo_full) then .– -- VHDL
In this case, you want to make sure that both the source FIFO has data (i.e., is not empty) and that the destination is not full. We can accomplish this by testing it via the if statement.
Logical OR
Another common occurrence is to check whether any one signal out of a group is set to perform an operation. An OR gate tests two or more inputs to determine if any of them are set to a 1. If any input is a 1, then the output will be a 1. If all inputs are 0, then the output is a 0.
The function in SystemVerilog/Verilog can be written as follows:
assign out = in1 || in0; // logical Boolean operator
The function in VHDL can be written as follows:
out <= in1 or in0; // logical Boolean operator
The associated truth table is as follows:
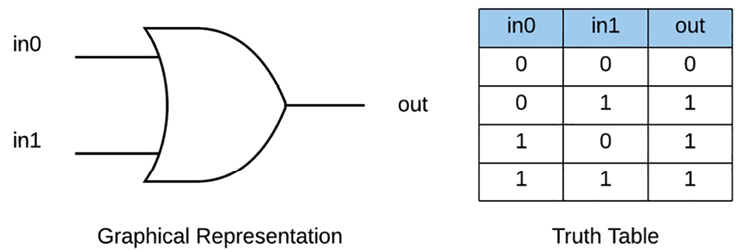
Figure 1.4: OR gate representation
Next, we will look at the exclusive OR function.
XOR
The exclusive OR (XOR) function checks whether either one of two inputs is set, but not both. XOR functions test whether an odd number of inputs are set to a 1 if you have more than two inputs.
The function in SystemVerilog/Verilog can be written as follows:
assign out = in1 ^ in0; // XOR Boolean operator
The function in VHDL can be written as follows:
out <= in1 xor in0; -- XOR Boolean operator
The associated truth table is as follows:
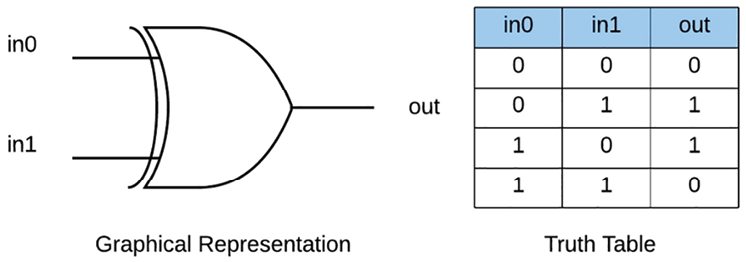
Figure 1.5: XOR gate representation
This function is used in building adders, parity, and error-checking and correcting code. In the next section, we’ll look at how an adder is built using the preceding gates.
More complex operations
We’ve seen the basic building blocks in the previous sections that make up every digital design. Here, we’ll look at an example of how we can put together multiple logic gates to perform work. For this, we will introduce the concept of a full adder. A full adder takes three inputs, A, B, and carry in (Cin), and produces two outputs, Sum and Carry out (Cout). Let’s look at the truth table of a full adder.
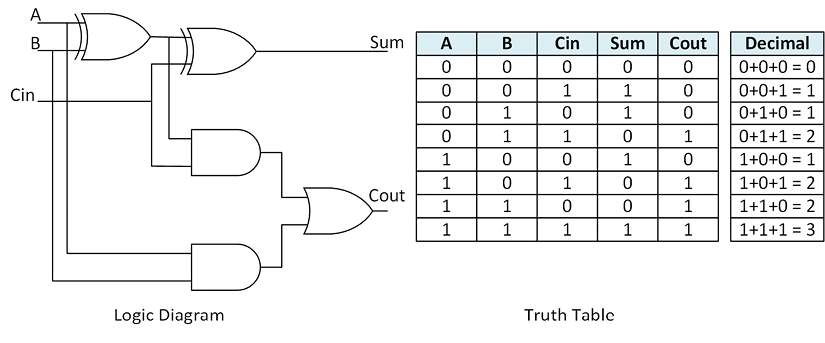
Algebraically, a full adder represents A + B + Cin. Each input is a single bit, so the output could be 0, 1, or 2 in decimal. Since we can only represent 0 and 1 in a single bit, if the addition produces a result of 2, that represents a carry out. The carry out would propagate into the next bit. This cascading of full adders is called a ripple carry adder, since they carry ripples from one cell to the next.
The SystemVerilog/ Verilog for the full adder written as Boolean logic would be as follows:
assign Sum = A ^ B ^ Cin;
assign Cout = A & B | (A ^ B) & Cin;
You’ll notice that we are using the bitwise operators for AND (&) and OR (|) since we are operating on bits. These are equivalent to the logical operators AND (&&) and OR (||). This is true for SystemVerilog/Verilog, but not in VHDL.
The VHDL code for the full adder written as Boolean logic would be as follows:
Sum <= A xor B xor Cin;
Cout <= (A and B) or ((A xor B) and Cin);
From this straightforward yet important example, you can see how real-world functionality can be built from these basic building blocks. All the circuits in an ASIC or FPGA are built this way, but luckily, you don’t need to dive into this level of detail unless you want to thanks to the proliferation of HDLs such as SystemVerilog/Verilog and VHDL.
With this basic understanding of gates and logic under our belts, we can look at FPGAs.


























































