Monte Carlo approximation
Monte Carlo experiments or sampling leverages randomness to solve mathematical or even deterministic problems [8:3]. There are three categories of problems:
Sampling from a given or empirical probability distribution
Optimization
Numerical approximation
This section focuses on the numerical integration.
Overview
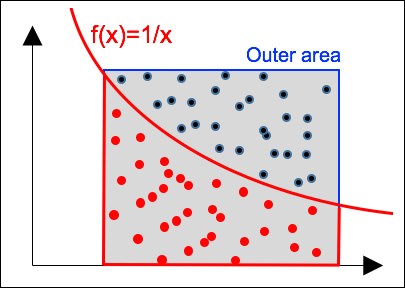
Let's apply the Monte Carlo simulation to numerical integration. the goal is to compute the area under a given single variable function [8:4]. The method consists of the following three-step process:
Define the outer area that is defined by the x axis and the maximum value of the function over the integration interval.
Generate a uniformly random distributed data point {x, y} over the outer area.
Count, then compute, the ratio of the number of data points under the function over the total number of random points.
The following diagram illustrates the three-step numerical integration for the function 1/x:
Monte Carlo numerical integration
Implementation
The MonteCarloApproximation...








































































