The NoSQL category of graph databases, as we have seen previously, is in a class of its own. In many ways, this is because the underlying data model of graph databases--the Property Graph data model--is of a very specific nature, which we will explain a bit further.
First of all, let's define the Property Graph data model. Essentially, it means that we will be storing our data in the graph database.
A graph structure means that we will be using vertices and edges (or nodes and relationships, as we prefer to call these elements) to store data in a persistent manner. As a consequence, the graph structure enables us to perform the following:
- Represent data in a much more natural way, without some of the distortions of the relational data model
- Apply various types of graph algorithms on these structures
In short, it enables us to treat the graph nature of that data as an essential part of our capabilities. One of the key capabilities that we will find in the remainder of this book is the capability to traverse the graph: to walk on its nodes and relationships and hop from one node to the next by following the explicit pointers that connect the nodes. This capability--sometimes also referred to as index free adjacency, which essentially means that you can find adjacent/neighbouring nodes without having to do an index lookup--is key to the performance characteristics that we will discuss in later paragraphs.
However, it is important to realize that the property graph model is not suited for all graph structures. Specifically, it is optimized for the following:
- Directed graphs: The links between nodes (also known as the relationships) have a direction.
- Multirelational graphs: There can be multiple relationships between two nodes that are the same. These relationships, as we will see later, will be clearly distinct and of a different type.
- Storing key-value pairs as the properties of the nodes and relationships.
In the different kinds of properties that can belong to the different elements of the graph structure, the most basic ones, of course, are properties assigned to vertices and edges:
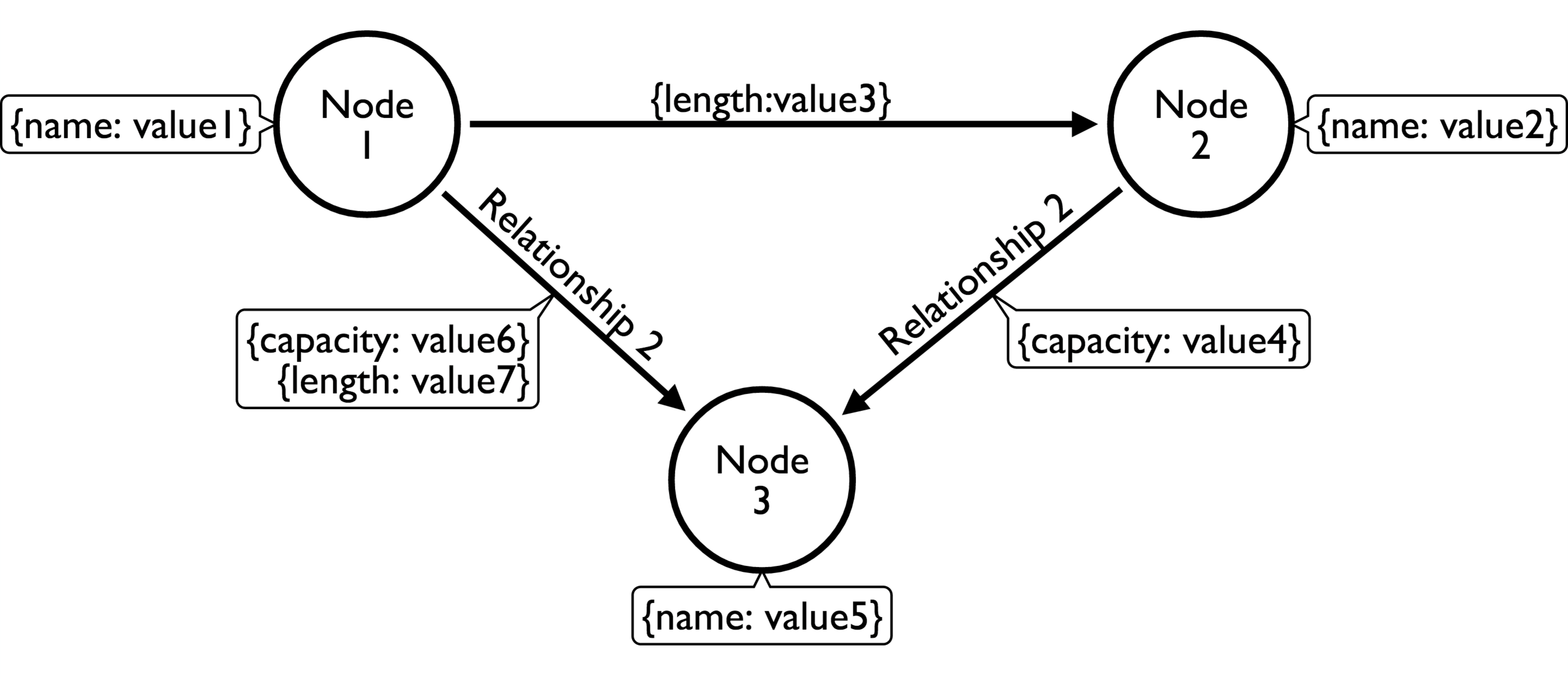
Let's investigate this model in a bit more detail. When looking closer at this, we find the following interesting aspects of this model:
- There is no fixed schema. The database, in and of itself, does not impose that you have to have a schema; although most software professionals will agree that having some kind of schema as you move closer to production is probably not a bad idea.
- Partly because of the schema-less nature of the database, it seems to be a very nice fit for dealing with semi-structured data. If one node or relationship has fewer or more properties, we do not have to alter the design for this; we can just deal with that difference in structure automatically and work with it in exactly the same way.
- Nodes and node properties seem to be quite easy to understand. In relational terms, one can easily compare nodes with records in a table. It's as if the property graph contains lots and lots of single-row tables, that is, the nodes of the graph. Nodes will have properties just like records/rows in a table will have fields/columns.
- Relationships are a bit different. They always have a start and endpoint, and therefore have a direction. They cannot be dangling, but can be self-referencing (the same node as the start and endpoint). However, the real power lies in the following facts:
- Relationships are explicit: They are not inferred by some kind of constraint or established at query time through a join operation. They are equal citizens in the database; they have the same expressive power as the nodes representing the entities in the database.
- Relationships can have properties too: They can have values associated with them that can specify the length, capacity, or any other characteristic of that relationship. This is terribly important and very different from anything we know from the relational world.
In Neo4j then, this data model has been enriched with a couple of key concepts that extend the core property graph model. Two concepts are important, and related but different: node labels and relationship types.




































































