In RL, the agent learns from the environment by interpreting the state signal. The state signal from the environment needs to define a discrete slice of the environment at that time. For example, if our agent was controlling a rocket, each state signal would define an exact position of the rocket in time. State, in that case, may be defined by the rocket's position and velocity. We define this state signal from the environment as a Markov state. The Markov state is not enough to make decisions from, and the agent needs to understand previous states, possible actions, and any future rewards. All of these additional properties may converge to form a Markov property, which we will discuss further in the next section.
Introducing the Markov decision process
The Markov property and MDP
An RL problem fulfills the Markov property if all Markov signals/states predict a future state. Subsequently, a Markov signal or state is considered a Markov property if it enables the agent to predict values from that state. Likewise, a learning task that is a Markov property and is finite is called a finite Markov decision process, or MDP. A very classic example of an MDP used to often explain RL is shown here:
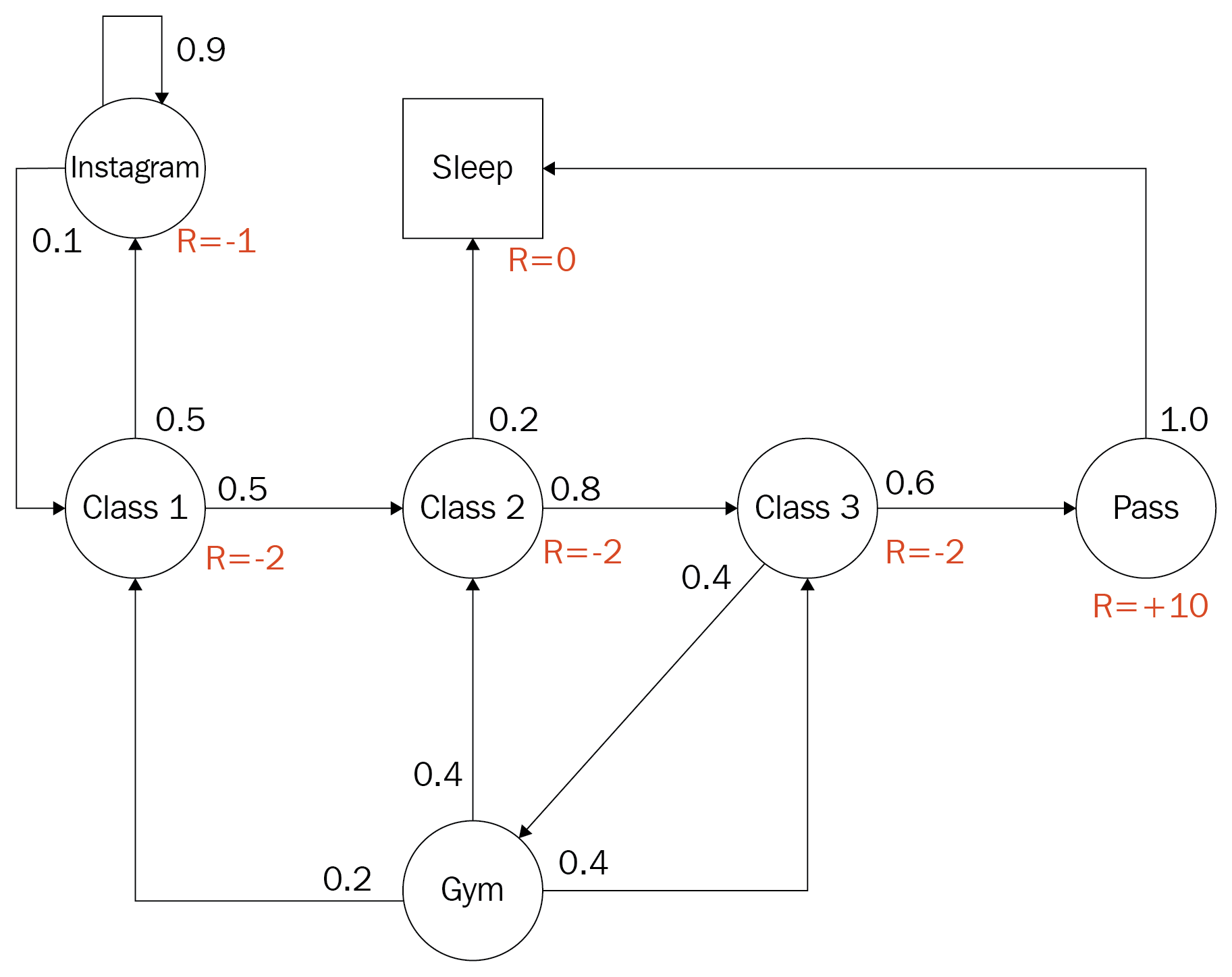
The Markov decision process (Dr. David Silver)
The diagram is an example of a finite discrete MDP for a post-secondary student trying to optimize their actions for maximum reward. The student has the option of attending class, going to the gym, hanging out on Instagram or whatever, passing and/or sleeping. States are denoted by circles and the text defines the activity. In addition to this, the numbers next to each path from a circle denote the probability of using that path. Note how all of the values around a single circle sum to 1.0 or 100% probability. The R= denotes the reward or output of the reward function when the student is in that state. To solidify this abstract concept further, let's build our own MDP in the next section.
Building an MDP
In this hands-on exercise, we will build an MDP using a task from your own daily life or experience. This should allow you to better apply this abstract concept to something more tangible. Let's begin as follows:
- Think of a daily task you do that may encompass six or so states. Examples of this may be going to school, getting dressed, eating, showering, browsing Facebook, and traveling.
- Write each state within a circle on a full sheet of paper or perhaps some digital drawing app.
- Connect the states with the actions you feel most appropriate. For example, don't get dressed before you shower.
- Assign the probability you would use to take each action. For example, if you have two actions leaving a state, you could make them both 50/50 or 0.5/0.5, or some other combination that adds up to 1.0.
- Assign the reward. Decide what rewards you would receive for being within each state and mark those on your diagram.
- Compare your completed diagram with the preceding example. How did you do?
Before we get to solving your MDP or others, we first need to understand some background on calculating values. We will uncover this in the next section.































































