Interpolating vectors
Two vectors can be interpolated linearly by scaling the difference between the two vectors and adding the result back to the original vector. This linear interpolation is often abbreviated to lerp. The amount to lerp by is a normalized value between 0 and 1; this normalized value is often represented by the letter t. The following figure shows lerp between two vectors with several values for t:

Figure 2.13: Linear interpolation
When t = 0, the interpolated vector is the same as the starting vector. When t = 1, the interpolated vector is the same as the end vector.
Implement the lerp function in vec3.cpp. Don't forget to add the function declaration to vec3.h:
vec3 lerp(const vec3 &s, const vec3 &e, float t) {
return vec3(
s.x + (e.x - s.x) * t,
s.y + (e.y - s.y) * t,
s.z + (e.z - s.z) * t
);
}
Linearly interpolating between two vectors will always take the shortest path from one vector to another. Sometimes, the shortest path isn't the best path; you may need to interpolate between two vectors along the shortest arc, instead. Interpolating on the shortest arc is called a spherical linear interpolation (slerp). The following figure shows the difference between the slerp and lerp processes for several values of t:
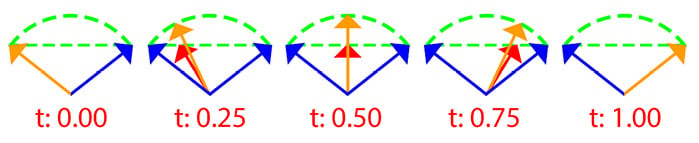
Figure 2.14: Comparing slerp and lerp
To implement slerp, find the angle between the two input vectors. Assuming the angle is known, the formula for slerp is as follows
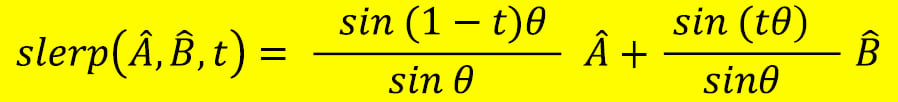
Implement the slerp function in vec3.cpp. Don't forget to add the function declaration to vec3.h. Take care of when the value of t is close to 0, as slerp will yield unexpected results. When the value of t is close to 0, fall back on lerp or normalized lerp (nlerp) (which will be covered next):
vec3 slerp(const vec3 &s, const vec3 &e, float t) {
if (t < 0.01f) {
return lerp(s, e, t);
}
vec3 from = normalized(s);
vec3 to = normalized(e);
float theta = angle(from, to);
float sin_theta = sinf(theta);
float a = sinf((1.0f - t) * theta) / sin_theta;
float b = sinf(t * theta) / sin_theta;
return from * a + to * b;
}
The last interpolation method to cover is nlerp. nlerp approximates slerp. Unlike slerp, nlerp is not constant in velocity. nlerp is much faster than slerp and easier to implement; just normalize the result of lerp. The following figure compares lerp, slerp, and nlerp, where t = 0.25:

Figure 2.15: Comparing lerp, slerp, and nlerp
Implement the nlerp function in vec3.cpp. Don't forget to add the function declaration to vec3.h:
vec3 nlerp(const vec3 &s, const vec3 &e, float t) {
vec3 linear(
s.x + (e.x - s.x) * t,
s.y + (e.y - s.y) * t,
s.z + (e.z - s.z) * t
);
return normalized(linear);
}
Generally, nlerp is a better choice than slerp. It's a very close approximation and much cheaper to calculate. The only time it makes sense to use slerp instead is if constant interpolation velocity is required. Throughout this book, you will be using lerp and nlerp to interpolate between vectors.
In the next section, you will learn how to use an epsilon value to compare vectors for equality and inequality.








































































