Dot product
The dot product, sometimes referred to as scalar product or inner product between two vectors, returns a scalar value. It's written as a dot between two vectors,  . The formula for the dot product is defined as follows:
. The formula for the dot product is defined as follows:

The sigma symbol  means sum (add) everything up that follows. The number on top of the sigma is the upper limit; the variable on the bottom is the lower limit. If n and i is 0, the subscripts 0, 1, and 2 are processed. Without using the sigma symbol, the preceding equation would look like this:
means sum (add) everything up that follows. The number on top of the sigma is the upper limit; the variable on the bottom is the lower limit. If n and i is 0, the subscripts 0, 1, and 2 are processed. Without using the sigma symbol, the preceding equation would look like this:
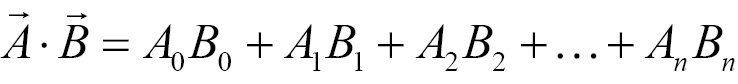
The resulting scalar represents the directional relation of the vectors. That is,  represents how much
represents how much  is pointing in the direction of
is pointing in the direction of  . Using the dot product we can tell if two vectors are pointing in the same direction or not following these rules:
. Using the dot product we can tell if two vectors are pointing in the same direction or not following these rules:
- If the dot product is positive, the vectors are pointing in the same direction
- If the dot product is negative, the vectors point in opposing directions
- If the dot product is 0, the vectors are perpendicular
How to do it…
Follow these steps to implement the dot product for two and three dimensional vectors:
- Add the declaration for the dot product to
vectors.h:float Dot(const vec2& l, const vec2& r); float Dot(const vec3& l, const vec3& r);
- Add the implementation for the dot product to
vector.cpp:float Dot(const vec2& l, const vec2& r) { return l.x * r.x + l.y * r.y; } float Dot(const vec3& l, const vec3& r) { return l.x * r.x + l.y * r.y + l.z * r.z; }
How it works…
Given the formula and the code for the dot product, let's see an example of what we could use it for. Assume we have a spaceship S. We know its forward vector,  and a vector that points to its right,
and a vector that points to its right,  :
:

We also have an enemy ship E, and a vector that points from our ship S to the enemy ship E, vector  :
:

How can we tell if the the ship S needs to turn left or right to face the enemy ship E?
We need to take the dot product of  and
and  . If the result of the dot product is positive, the ship needs to turn right. If the result of the dot product is negative, the ship needs to turn to the left. If the result of the dot product is 0, the ship does not need to turn.
. If the result of the dot product is positive, the ship needs to turn right. If the result of the dot product is negative, the ship needs to turn to the left. If the result of the dot product is 0, the ship does not need to turn.
There's more…
Our definition of the dot product is fairly abstract. We know that the dot product gives us some information as to the angle between the two vectors,  and
and  . We can use the dot product to find the exact angle between these two vectors. The key to this is an alternate definition of the dot product.
. We can use the dot product to find the exact angle between these two vectors. The key to this is an alternate definition of the dot product.
Geometric definition
Given the vectors  and
and  , the geometric definition of the dot product is the length of
, the geometric definition of the dot product is the length of  multiplied by the length of
multiplied by the length of  multiplied by the cosine of the angle between them:
multiplied by the cosine of the angle between them:

The || operator in the above equation means length and will be covered in the next section. We will cover the geometric definition and other properties of the dot product later in this chapter.




























































