Understanding mean, median, and mode
Mean, median, and mode describe the central tendency in some way. Mean and median are only applicable to numerical variables whereas mode is applicable to both categorical and numerical variables. In this section, we will be focusing on mean, median, and mode for numerical variables as their numerical interactions usually convey interesting observations.
Mean
Mean, or arithmetical mean, measures the weighted center of a variable. Let's use n to denote the total number of entries and 
as the index. The mean 
reads as follows:
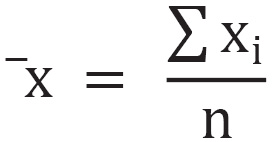
Mean is influenced by the value of every entry in the population.
Let me give an example. In the following code, I will generate 1,000 random numbers from 0 to 1 uniformly, plot them, and calculate their mean:
import random
random.seed(2019)
plt.figure(figsize=(8,6))
rvs = [random.random() for _ in range(1000)]
plt.hist(rvs, bins=50)
plt.title("Histogram of Uniformly Distributed...
