7.4 A nonlinear projection
In Chapter 5, “Dimensions,” we saw linear projections, such as mapping any point in the real plane to the line y = x. Now, we look at a special kind of projection that is nonlinear. We map almost every point on the unit circle onto a line. We will use this in the next section when we discuss the Bloch sphere.
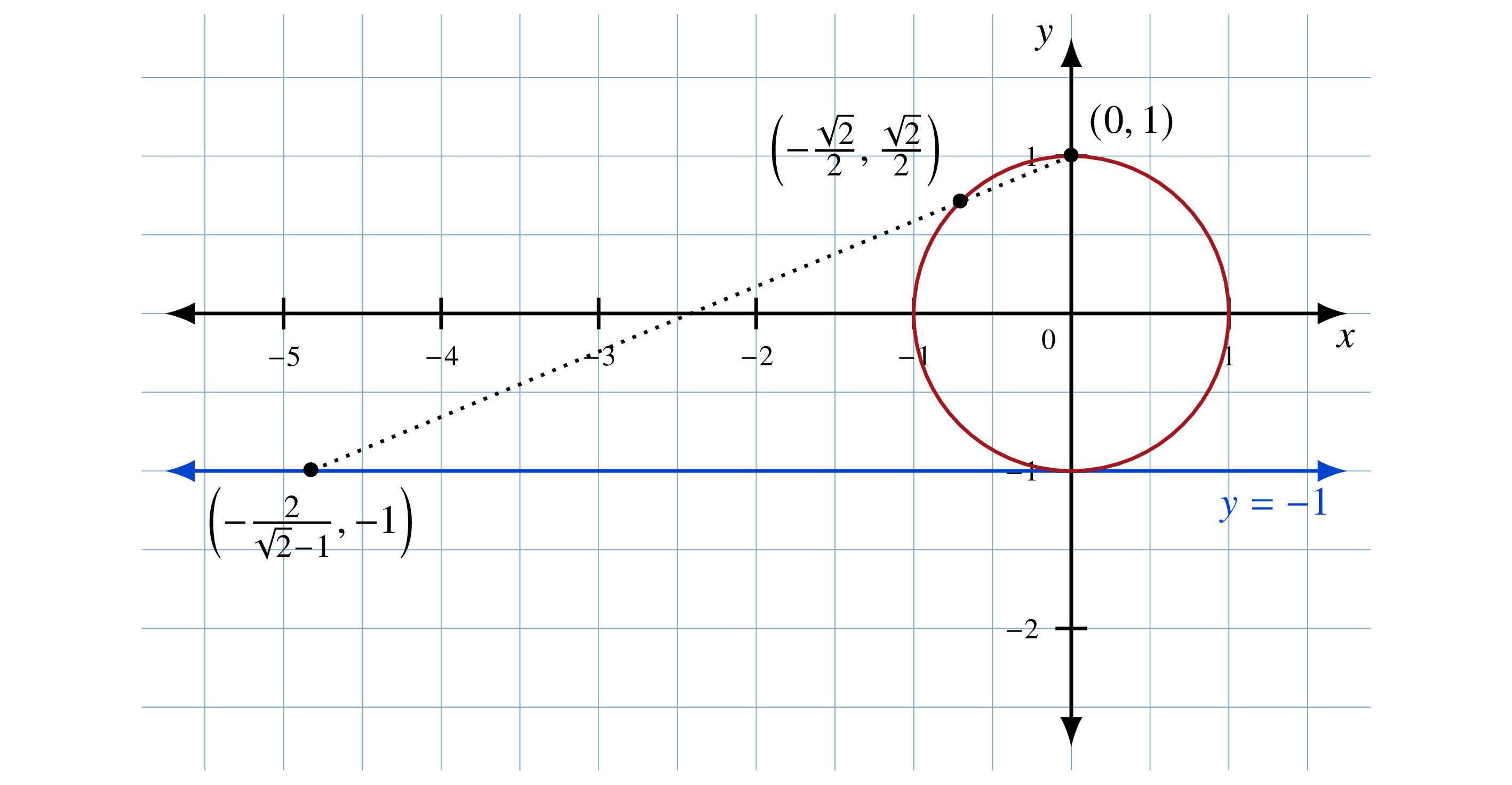
Figure 7.3 shows a unit circle and the line y = –1 that sits right below it.
We can map every point on the circle except (0, 1), the north pole, to a point on the line y = –1. We simply draw a line from (0, 1) through the point on the circle. The result is where that line intersects y = –1, as shown in Figure 7.4. The south pole maps to itself. We want different points on the circle to map to different points on the line.