Separating Nonlinear boundaries with Support vector machines

In our previous example of logistic regression, we assumed implicitly that every point in the training set might be useful in defining the boundary between the two classes we are trying to separate. In practice we may only need a small number of data points to define this boundary, with additional information simply adding noise to the classification. This concept, that classification might be improved by using only a small number of critical data points, is the key features of the support vector machine (SVM) model.

In its basic form, the SVM is similar to the linear models we have seen before, using the following equation:

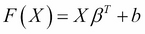
where b is an intercept, and β is the vector of coefficients such as we have seen in regression models. We can see a simple rule that a point X is classified as class 1 if F(x) ≥ 1, and class -1 if F(x) ≤ –1. Geometrically, we can understand this as the distance from the plane to the point x, where β is a vector...