LR is an algorithm for classification, which predicts a binary response. It is similar to linear regression, which we described in Chapter 2, Scala for Regression Analysis, except that it does not predict continuous values—it predicts discrete classes. The loss function is the sigmoid function (or logistic function):
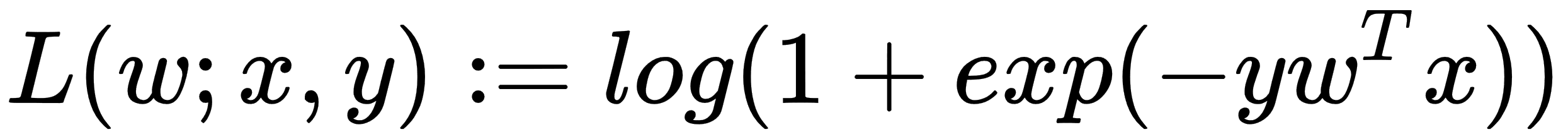
Similar to linear regression, the intuition behind the cost function is to penalize models that have large errors between the real response and the predicted response:
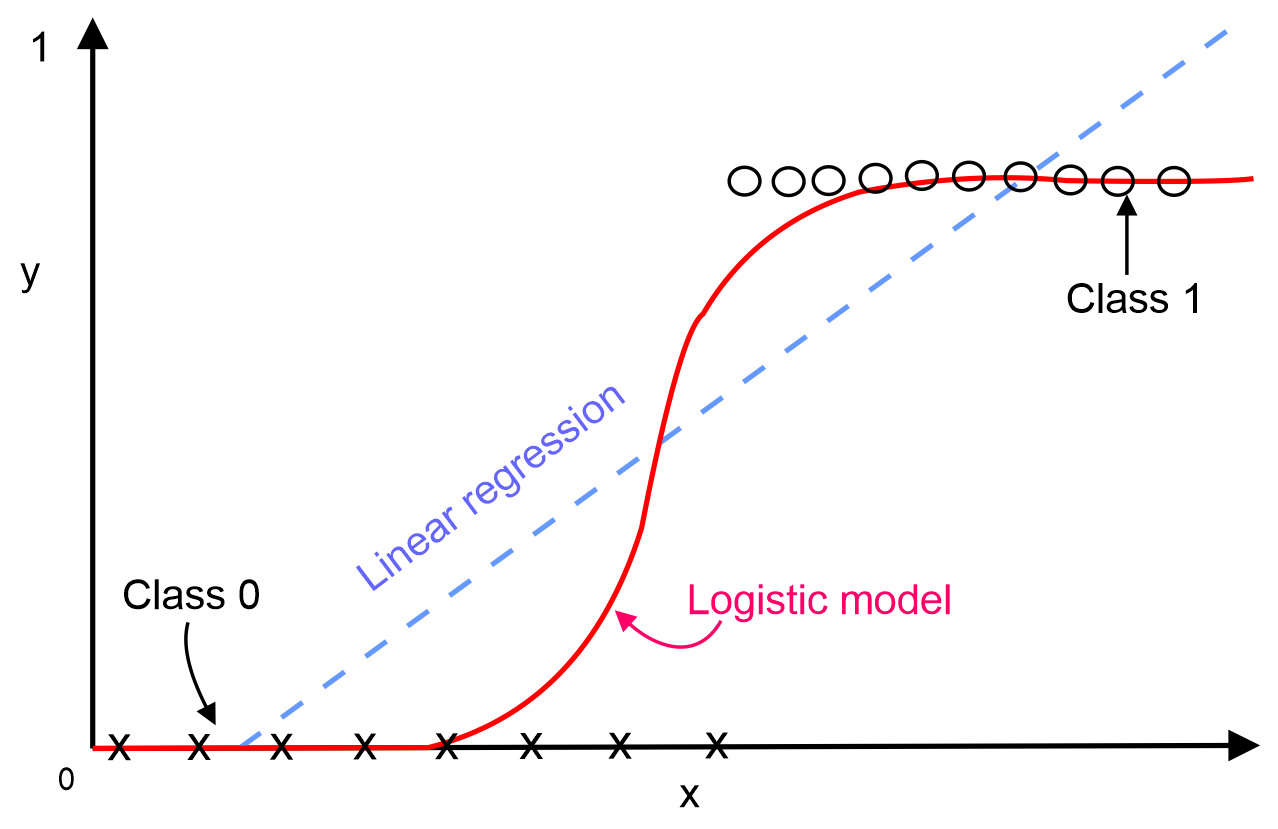
For a given new data point, x, the LR model makes predictions using the following equation:
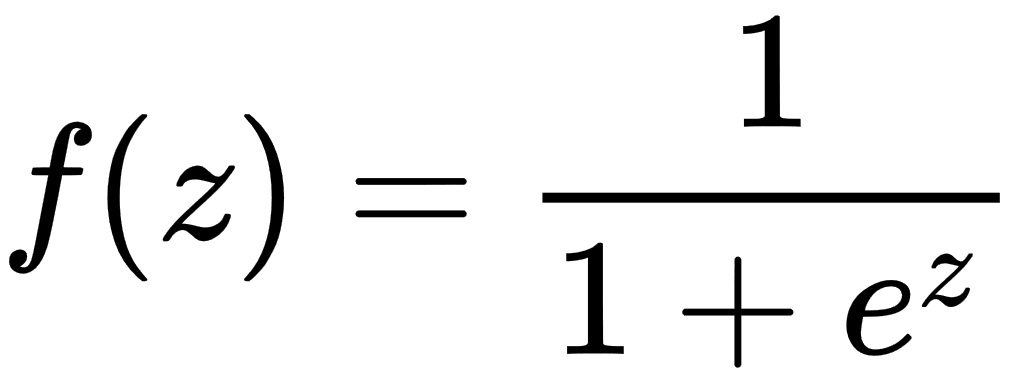
In the preceding equation, the logistic function is applied to the regression to get the probabilities of it belonging in either class, where z = wT x and if f(wT x) > 0.5, the outcome is positive; otherwise, it is negative. This means that the threshold for the classification...












































































