Higher level of abstraction
FP allows us to work at a higher level of abstraction. Abstraction is selective ignorance. The world we know of runs on abstractions. If we say, "Give me sweet condensed milk frozen with embedded dry fruits' someone might really have a hard time understanding it. Instead, just say "ice-cream"! Aha! It just falls into place and everyone is happy.
Abstractions are everywhere. An airplane is an abstraction, so is a sewing machine or a train. When we wish to travel by train, we buy a ticket, board the train, and get off at the destination. We really don't worry about how the train functions. We simply can't be expected to deal with all the intricacies of a train engine. As long as it serves our purpose, we ignore details related to how an engine really works.
What are the benefits of an abstraction? We don't get bogged down into unnecessary details. Instead, we focus on the task at hand by applying higher level programming abstractions.
Compare the preceding for loop with the functional code snippet:
scala> val x = Array(1,2,3,4,5,6) x: Array[Int] = Array(1, 2, 3, 4, 5, 6) scala> x.foreach(println _) 1 2 ...
We simply focus on the task at hand (print each element of an array) and don't care about the mechanics of a for loop. The functional version is more abstract.
As software engineers, when we implement an algorithm and run it, we are intentionally ignoring many details.
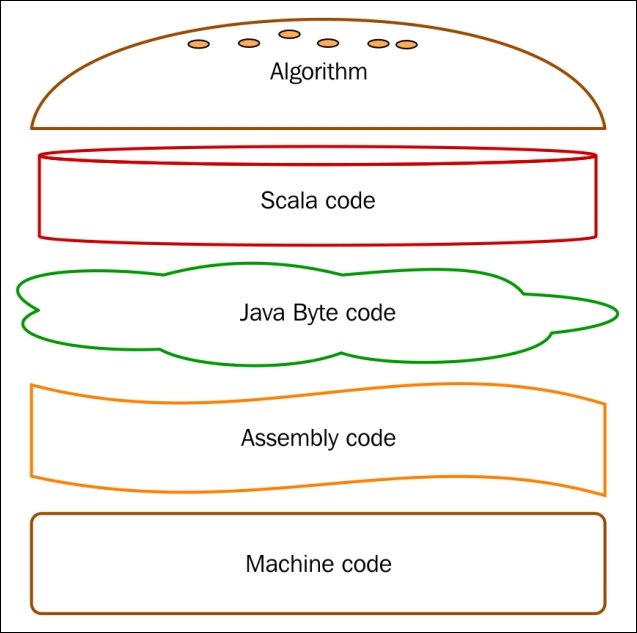
We know that the preceding sandwich stack somehow works and faithfully translates the algorithm into runnable code.
Applying higher level abstractions is commonly done in functional languages. For example, consider the following Clojure REPL snippet:
user=> ((juxt (comp str *) (comp str +)) 1 2 3 4 5) ["120" "15"]
We are juxtaposing two functions; each of these are in turn composed of the str function and an arithmetic function:
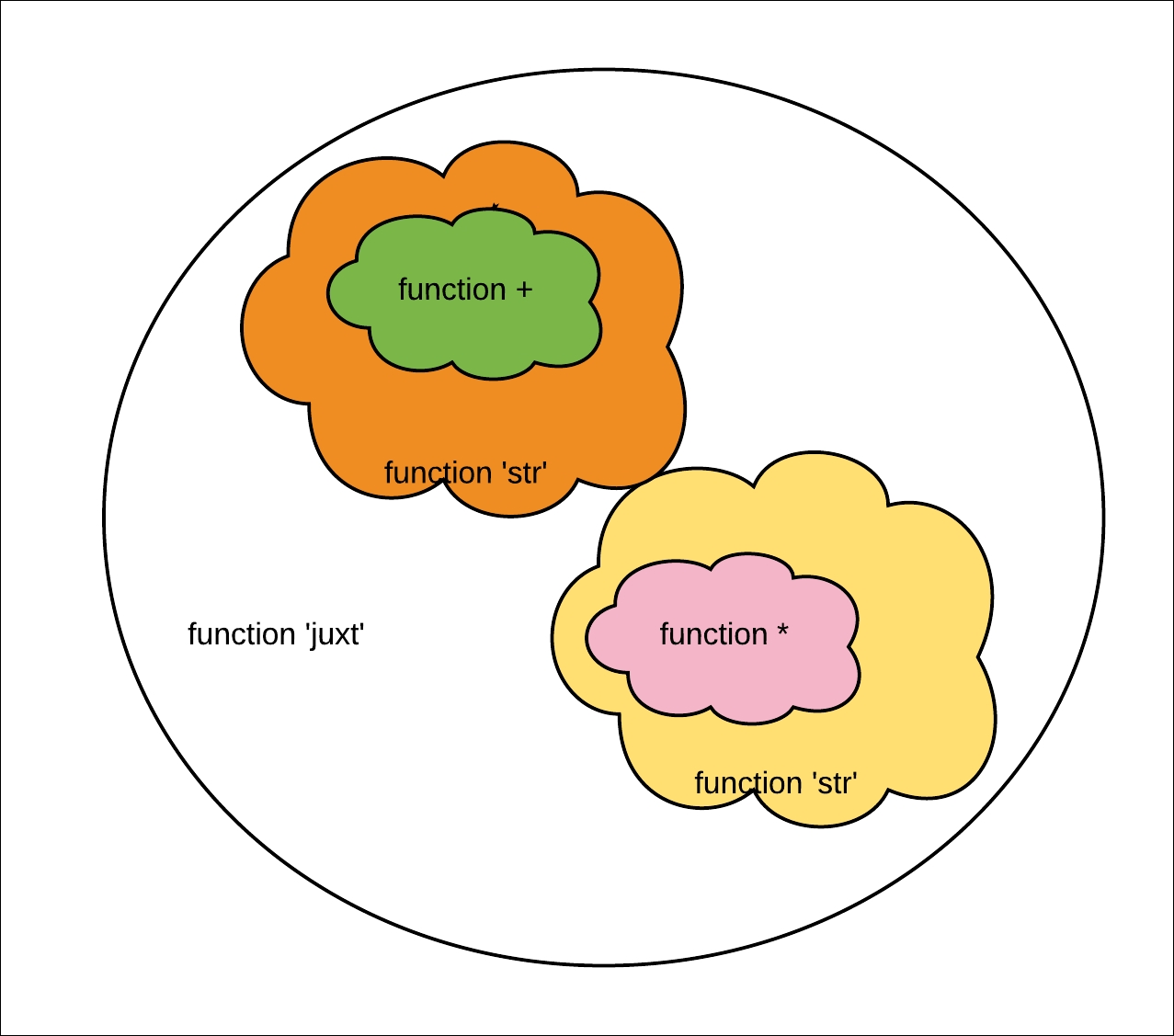
We just don't worry about how it works internally. We just use high-level abstractions cobbled together with existing pieces of abstract functionality.
We will be looking at abstract data types (ADT) closely in this book. For example, when we talk about a stack, we think of the Last In First Out (LIFO) order of access. However, this ADT is realized by implementing the stack via a data structure, such as a linked list or an array.
Here is a figure showing the First In First Out (FIFO) ADT in action. The FIFO queue is the normal queue we encounter in life, for example, queuing up at a booking counter. The earlier you get into a queue, the sooner you get serviced.
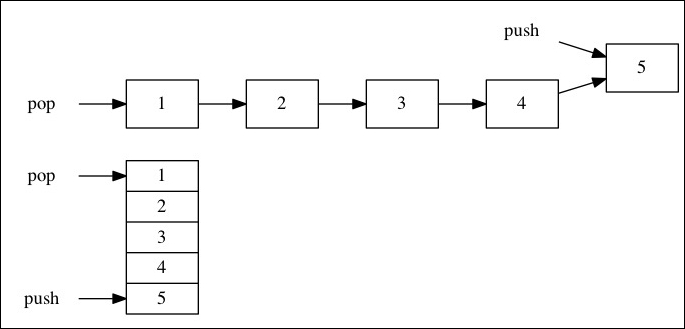
The FIFO queue is an ADT. True that we think of it as an ADT; however, as shown in the preceding diagram, we can also implement the queue backed by either an array or a linked list.




























































