Composing functions
We programmers, love reusing code. We use libraries and frameworks, so we use something that already exists out there. No one wants to reinvent the same wheel again. For example, here is how we could weed out zeroes from a Clojure vector:
user=> (filter (complement zero?) [0 1 2 0 3 4]) (1 2 3 4)
The following diagram shows the functional composition:
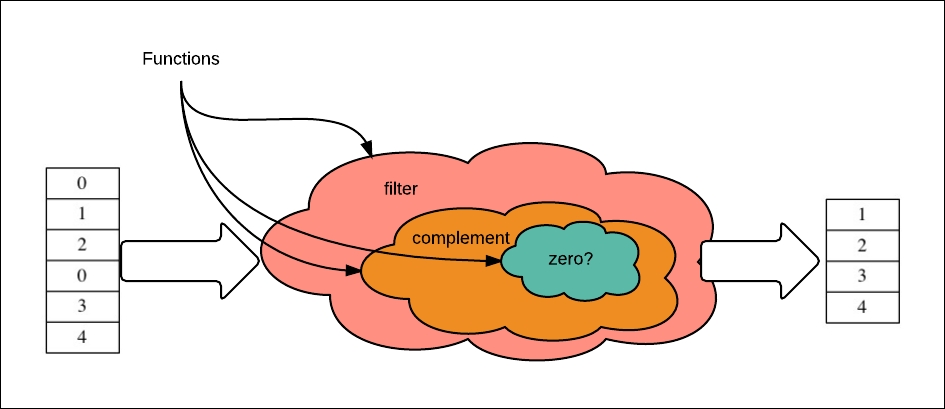
We composed behavior by composing predicate functions; we did this using complement to negate the zero? predicate function. The zero? predicate returns true if its input is 0; if not, it returns false.
Given a list of numbers, the following Scala snippet checks whether the sequence is strictly increasing:
scala> val x = List(1, 2, 3, 4, 5, 6, 7) x: List[Int] = List(1, 2, 3, 4, 5, 6, 7) scala> val y = x zip x.drop(1) y: List[(Int, Int)] = List((1,2), (2,3), (3,4), (4,5), (5,6), (6,7)) scala> y forall (x => x._1 < x._2) res2: Boolean = true
Just imagine how we would do this in an imperative language.
Using zip, we get each number and its successor as a pair. We pass in a function to know whether the first element of the pair is less than the second.
Here goes the Clojure implementation. First we define a function that takes a list of two elements, de-structures it into its elements, and checks whether these two elements are strictly increasing:
user=> (defn check? [list] #_=> (let [[x y] list] #_=> (> y x)))
Here is a quick test:
user=> (check? '(21 2)) false user=> (check? '(1 2)) true
Tip
Note that the check? function is a pure function. It works just on its input and nothing else.
Next comes the pair generation; here, each element is paired with its successor:
user=> (defn gen-pairs [list] #_=> (let [x list #_=> y (rest list)] #_=> (partition 2 (interleave x y))))
Testing it gives the following:
user=> (gen-pairs '(1 2 3 4)) ((1 2) (2 3) (3 4))
Now comes the magic! We compose these two functions to check whether the input is strictly increasing:
user=> (defn strictly-increasing? [list] #_=> (every? check? (gen-pairs list))) #'user/strictly-increasing?
Testing it gives the following:
user=> (strictly-increasing? '(1 2 3 4)) true user=> (strictly-increasing? '(1 2 3 4 2)) false
See how succinct it becomes when we start composing functions:
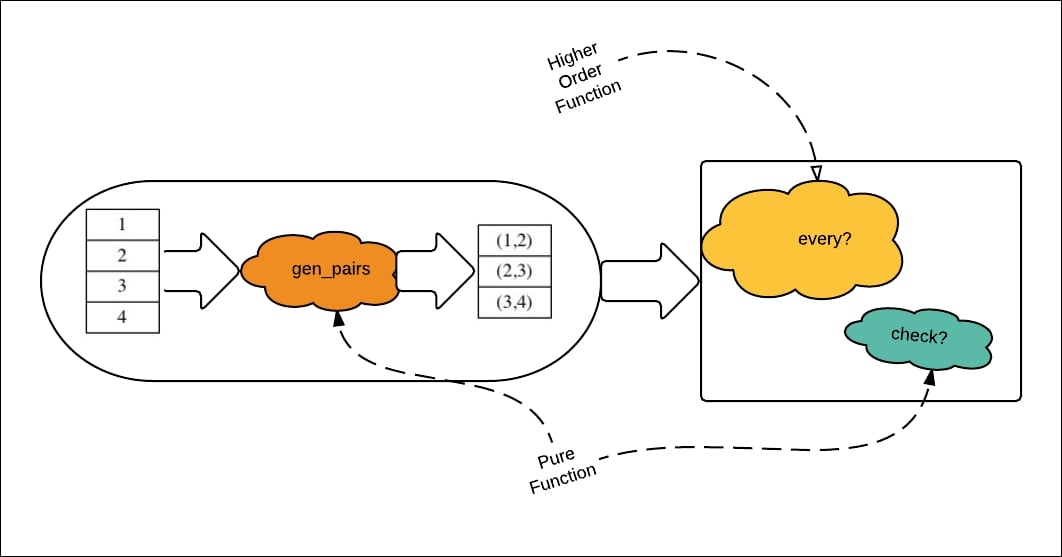
Note that the functions check? and every? are pure functions. The check? function predicate works on the input only. The gen_pairs is also a pure function. It is, in turn, composed of the interleave and partition functions.
The every? function is also a higher order function. We never wrote any loops (not even any recursion). We composed behavior out of existing pieces. The fun thing is the pieces don't need to know about the composition. We just combine independent processing pieces together.
For a great treatment of the advantages FP brings to the table, we wholeheartedly recommend Functional Thinking-- Paradigm Over Syntax (http://shop.oreilly.com/product/0636920029687.do ).




























































