Building trees with nodes

In this topic, you'll be learning how to create a search tree with nodes. We will look at the concepts of states and nodes and the properties and methods of the node class, and we will show you how to create a tree with node objects. In our application, while the state is the path of the file or folder we are processing (for example, the current directory), the node is a node in the search tree (for example, the current directory node).

A node has many properties, and one of them is the state. The other properties are as follows:

• Depth: This is the level of the node in the tree
• Reference to the parent node: This consists of links to the parent node
• References to the child nodes: This consists of links to the child nodes

Let's look at a few examples, in order to understand these concepts more clearly:

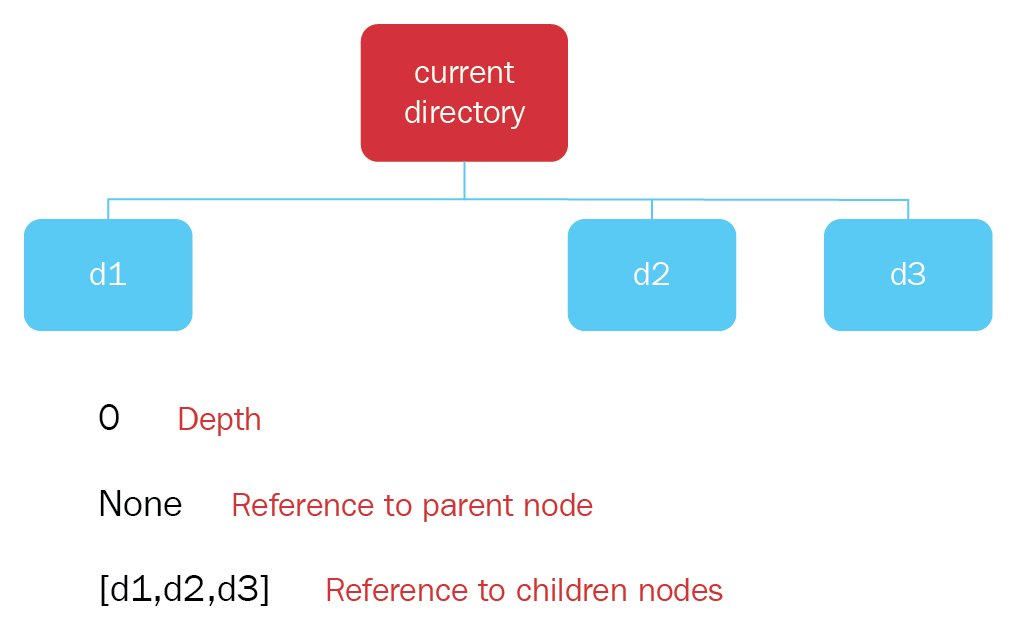
• An example of these concepts in the current directory node is as follows:
  • Depth: 0
  • Reference to parent node: None
  • References to children nodes: d1, d2, d3

Figure 20

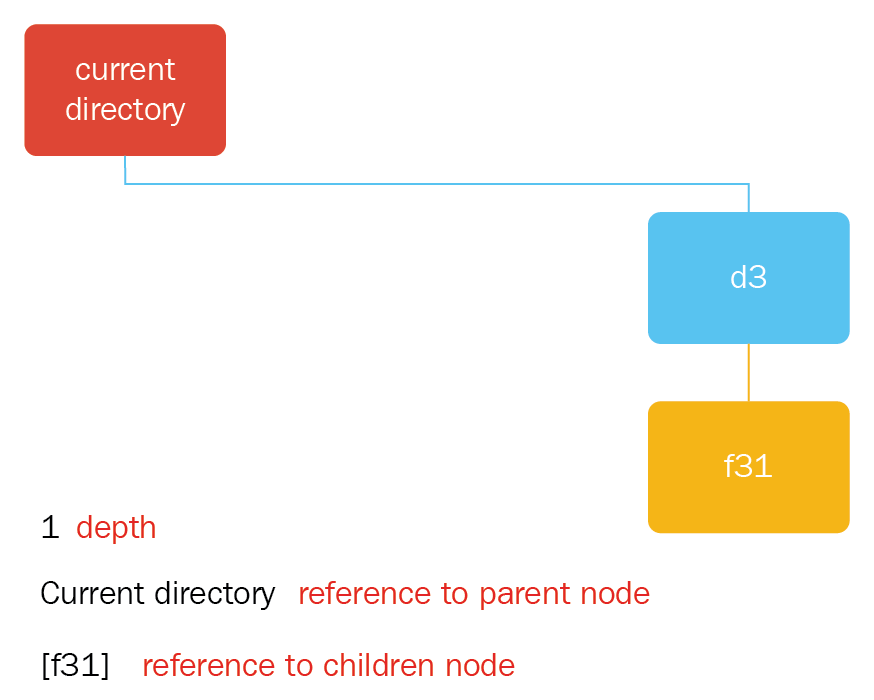
• An example of these concepts in node d3 is as follows:
  • Depth: 1
  • Reference to parent node: Current directory node
  • Reference to children nodes: f31

Figure 21

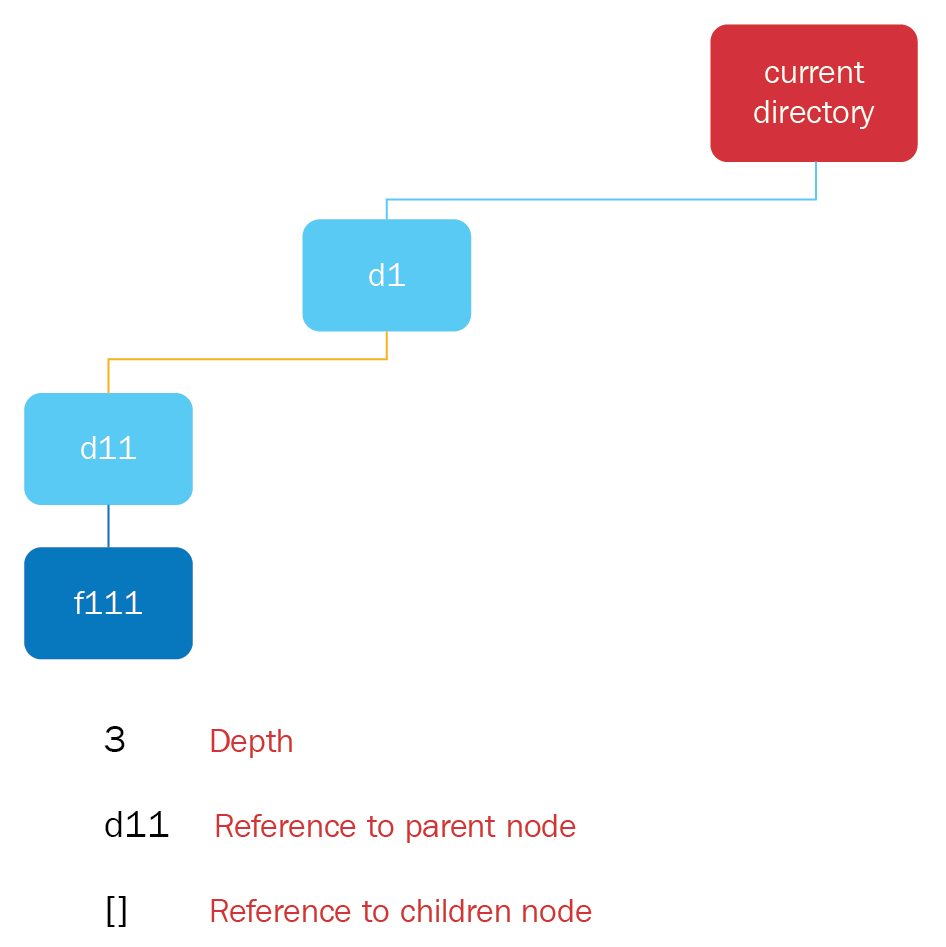
• An example of the concepts for these file node f111 is as follows:
  • Depth: 3
  • Reference to parent node: d11
  • Reference to children node: []

Figure 22

Let's create a class called Node, which includes the four properties that we just discussed:

...
class Node:
    '''
    This class represents a node in the search tree
    '''
    
    def __init__(self, state):
        """
        Constructor
        """
        self.state = state
        self.depth = 0
        self.children = []
        self.parent = None
...

As shown in the preceding code, we have created a class called Node, and this class has a constructor that takes state as an argument. The state argument is assigned to the state property of this node, and the other properties are initialized as follows:

• The depth is set to 0
• The reference to children is set to a blank array
• The reference to parent nodes is set to None

This constructor creates a blank node for the search tree.

Aside from the constructor, we need to create the following two methods:

• addChild(): This method adds a child node under a parent node
• printTree(): This method prints a tree structure

Consider the following code for the addChild() function:

def addChild(self, childNode):
        """
        This method adds a node under another node
        """
        self.children.append(childNode)
        childNode.parent = self
        childNode.depth = self.depth + 1

The addChild() method takes the child node as an argument; the child node is added to the children array, and the parent of the child node is assigned as its parent node. The depth of the child node is the parent node plus one.

Let's look at this in the form of a block diagram for a clearer understanding:

Figure 23

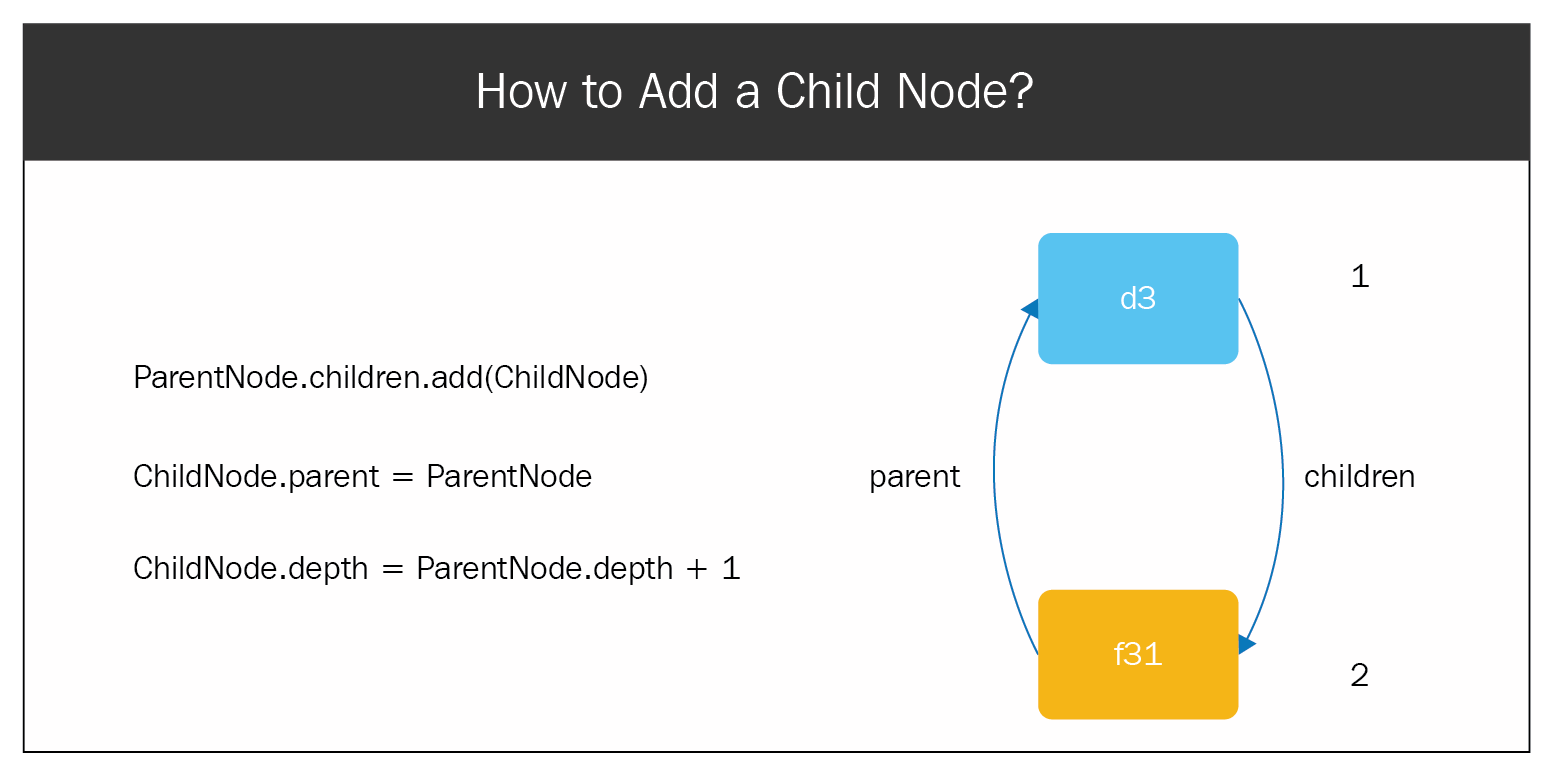
Let's suppose that we're adding node f31 under node d3. So, f31 will be added to the children property of d3, and the parent property of f31 will be assigned as d3. In addition to that, the depth of the child node will be one more than the parent node. Here, the depth of node d3 is 1, so the depth of f31 is 2.

Let's look at the printTree function, as follows:

def printTree(self):
        """
        This method prints the tree
        """
        print self.depth , " - " , self.state.path
        for child in self.children:
            child.printTree()

First, this function prints the depth and the state of the current node; then, it looks through all of its children and calls the printTree method for each of them.

Let's try to create the search tree shown in the following diagram:

Figure 24

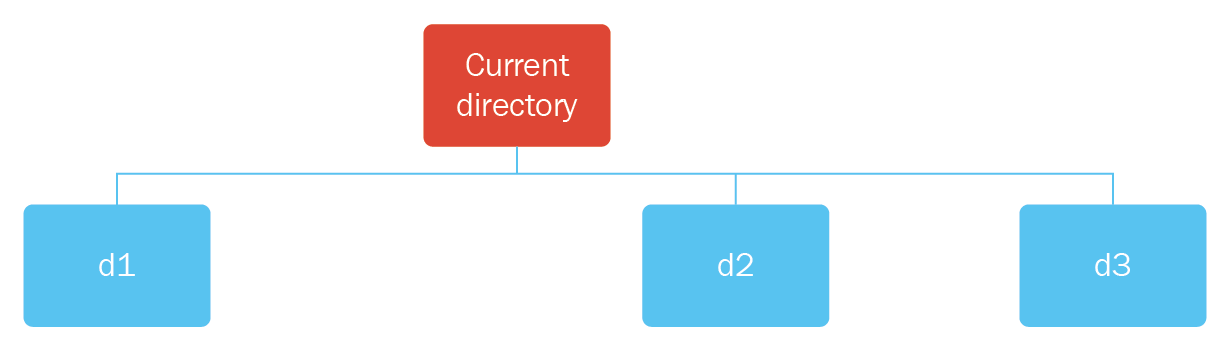
As shown in the preceding diagram, as a root node we have the Current directory node; under that node, we have nodes d1, d2, and d3.

We will create a NodeTest module, which will create the sample search tree:

...
from Node import Node
from State import State

initialState = State()
root = Node(initialState)

childStates = initialState.successorFunction()
for childState in childStates:
    childNode = Node(State(childState))
    root.addChild(childNode)
    
root.printTree()
...

As shown in the preceding code, we created an initial state by creating a State object with no arguments, and then we passed this initial state to the Node class constructor, which creates a root node. To get the folders d1, d2, and d3, we called the successorFunction method on the initial state and we looped each of the child states (to create a node from each of them); we added each child node under the root node.

When we execute the preceding code, we get the following output:

Figure 25

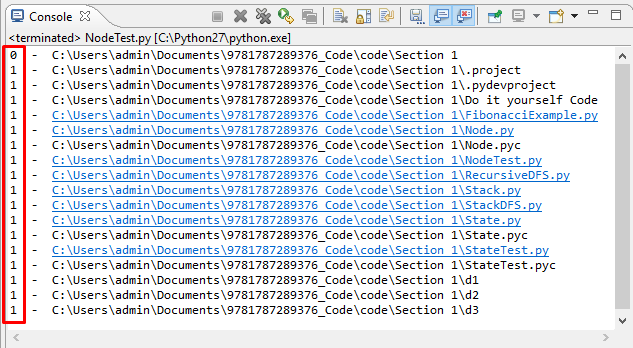
Here, we can see that the current directory has a depth of 0, and all of its contents have a depth 1, including d1, d2, and d3.

With that, we have successfully built a sample search tree using the Node class.

In the next topic, you'll be learning about the stack data structure, which will help us to create the DFS algorithm.