The t-statistic
While using the t-distribution, we look up the t-statistic. Like the z-statistic, this value quantifies how unlikely a particular observed deviation is. For a dual sample t-test, the t-statistic is calculated in the following way:

Here,  is the pooled standard error. We could calculate the pooled standard error in the same way as we did earlier:
is the pooled standard error. We could calculate the pooled standard error in the same way as we did earlier:
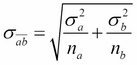
However, the equation assumes knowledge of the population parameters σa and σb, which can only be approximated from large samples. The t-test is designed for small samples and does not require us to make assumptions about population variance.
As a result, for the t-test, we write the pooled standard error as the square root of the sum of the standard errors:

In practice, the earlier two equations for the pooled standard error yield identical results, given the same input sequences. The difference in notation just serves to illustrate that with the t-test, we depend only on sample statistics as input. The pooled standard error  can be...
can be...






















































