What Is Dynamic Programming?
The best way to answer this question is by example. To illustrate the purpose of dynamic programming, let's consider the Fibonacci sequence:
{ 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … }
By observing the preceding sequence, we can see that, beginning with the third element, each term is equal to the sum of the two preceding terms. This can be simply expressed with the following formula:
F(0) = 0
F(1) = 1
…
F(n) = F(n-1) + F(n-2)
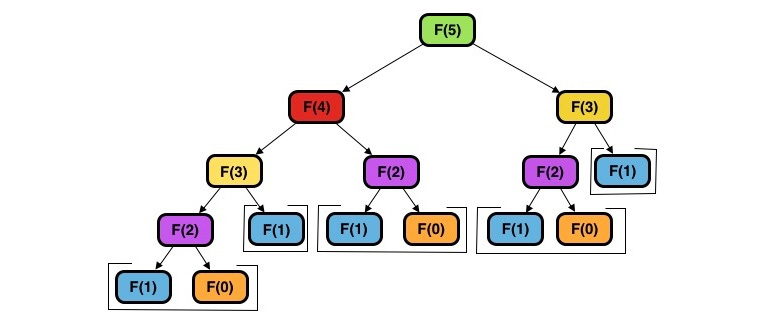
As we can clearly see, the terms of this sequence have a recursive relationship – the current term, F(n), is based on the results of previous terms, F(n-1) and F(n-2), and thus the preceding equation, that is, F(n) = F(n-1) + F(n-2), is described as the recurrence relation of the sequence. The initial terms, F(0) and F(1), are described as the base cases, or the points in which a solution is produced without the need to recurse further. These operations are shown in the following figure: