Packt+ | Advance your knowledge in tech

0

Explore Products

Best Sellers

New Releases

Books

Videos

Audiobooks

Free Learning

Applied Supervised Learning with R

You're reading from Applied Supervised Learning with R Use machine learning libraries of R to build models that solve business problems and predict future trends

Product type Paperback

Published in May 2019

Publisher

ISBN-13 9781838556334

Length 502 pages

Edition 1st Edition

Languages

R

Concepts

Machine Learning

Authors (2):

Jojo Moolayil

Karthik Ramasubramanian

View More author details

Table of Contents (12) Chapters

Applied Supervised Learning with R

Preface

1. R for Advanced Analytics FREE CHAPTER

2. Exploratory Analysis of Data

3. Introduction to Supervised Learning

4. Regression

5. Classification

6. Feature Selection and Dimensionality Reduction

7. Model Improvements

8. Model Deployment

9. Capstone Project - Based on Research Papers

Appendix

Poisson Regression

In linear regression, we saw an equation of the form:

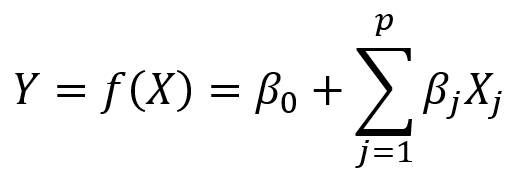
In Poisson Regression, the response variable Y is a count or rate (Y/t) that has a Poisson distribution with expected (mean) count of as , which is equal to variance.

In case of logistic regression, we would probe for values that can maximize log-likelihood to get the maximum likelihood estimators (MLEs) for coefficients.

There are no closed-form solutions, hence the estimations of maximum likelihood would be obtained using iterative algorithms such as Newton-Raphson and Iteratively re-weighted least squares (IRWLS).

Poisson regression is suitable for the count-dependent variable, which must meet the following guidelines:

It follows a Poisson distribution
Counts are not negative
Values are whole numbers (no fractions)

Note

The dataset used here to demonstrate Poisson regression comes from A. Colin Cameron and Per Johansson, "Count Data Regression Using Series Expansion: With Applications", Journal of Applied Econometrics, Vol...

The rest of the chapter is locked

Register for a free Packt account to unlock a world of extra content!

A free Packt account unlocks extra newsletters, articles, discounted offers, and much more. Start advancing your knowledge today.

Unlock this book and the full library FREE for 7 days

Get unlimited access to 7000+ expert-authored eBooks and videos courses covering every tech area you can think of

Start free trial

Renews at €18.99/month. Cancel anytime

Authors (2)

Karthik Ramasubramanian

Karthik Ramasubramanian

Karthik Ramasubramanian completed his M.Sc. in Theoretical Computer Science at PSG College of Technology, India, where he pioneered the application of machine learning, data mining, and fuzzy logic in his research work on computer and network security. He has over seven years' experience of leading data science and business analytics in retail, Fast-Moving Consumer Goods, e-commerce, information technology, and the hospitality industry for multinational companies and unicorn start-ups. He is a researcher and a problem solver with diverse experience of the data science life cycle, starting from data problem discovery to creating data science proof of concepts and products for various industry use cases. In his leadership roles, Karthik has been instrumental in solving many ROI-driven business problems via data science solutions. He has mentored and trained hundreds of professionals and students globally in data science through various online platforms and university engagement programs. He has also developed intelligent chatbots based on deep learning models that understand human-like interactions, customer segmentation models, recommendation systems, and many natural language processing models. He is an author of the book Machine Learning Using R, published by Apress, a publishing house of Springer Business+Science Media. The book was a big success with more than 50,000 online downloads and hardcover sales. The book was subsequently published as a second edition with extended chapters on Deep Learning and Time Series Modeling.

See other products by Karthik Ramasubramanian

Jojo Moolayil

Jojo Moolayil

Jojo Moolayil is an artiﬁcial intelligence, deep learning, machine learning, and decision science professional with over six years of industrial experience. He is the author of Learn Keras for Deep Neural Networks, published by Apress, and Smarter Decisions – The Intersection of IoT and Decision Science, published by Packt Publishing. He has worked with several industry leaders on high-impact, critical data science and machine learning projects across multiple verticals. He is currently associated with Amazon Web Services as a research scientist in Canada. Apart from writing books on AI, decision science, and the internet of things, Jojo has been a technical reviewer for various books in the same ﬁelds published by Apress and Packt Publishing.

See other products by Jojo Moolayil

Other recommended products

Related to this chapter

Practical Machine Learning with R

Practical Machine Learning with R

Practical Machine Learning with R gives you the complete knowledge to solve your business problems - starting by forming a good problem statement, selecting the most appropriate model to solve your problem, and then ensuring that you do not overtrain the model.

Aug 2019 13h 52m

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R puts the complete process of exploratory data analysis into a practical demonstration in one nutshell. You will understand the concepts of data analysis right from data ingestion, data cleaning, data manipulation to applying statistical techniques and visualizing hidden patterns.

May 2019 8h 52m

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R puts the complete process of exploratory data analysis into a practical demonstration in one nutshell. You will understand the concepts of data analysis right from data ingestion, data cleaning, data manipulation to applying statistical techniques and visualizing hidden patterns.

May 2019 8h 52m

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R

Hands-On Exploratory Data Analysis with R puts the complete process of exploratory data analysis into a practical demonstration in one nutshell. You will understand the concepts of data analysis right from data ingestion, data cleaning, data manipulation to applying statistical techniques and visualizing hidden patterns.

May 2019 8h 52m

Machine Learning with R Cookbook

Machine Learning with R Cookbook

The R language is a powerful open source functional programming language. At its core, R is a statistical language that provides impressive tools to analyze data and create high-level graphics. This book covers the basics of R by setting up a user-friendly programming environment and programming ETL in R. Data exploration examples are provided that demonstrate how powerful data visualisation and machine learning is in discovering hidden relationships. You will also explore air quality data, steps to fix the missing values and visualising the same. You will then dive into important machine learning topics, including data classification, regression, survival analysis, time series analysis, clustering association rule mining, and dimension reduction.This book will include the latest code and examples based on R 3.3 and above—updated for better computation, accuracy, and speed with R.

Oct 2017 19h 4m

Regression Analysis with R

Regression Analysis with R

Regression analysis is a statistical process which enables prediction of relationships between variables. This book will give you a rundown explaining what regression analysis is, explaining you the process from scratch. Each chapter starts with explaining the theoretical concepts and once the reader gets comfortable with the theory, we move to the practical examples to support the understanding. By the end of this book you will know all the concepts and pain-points related to regression analysis, and you will be able to implement your learning in your projects.

Jan 2018 14h 4m

Regression Analysis with R

Regression Analysis with R

Regression analysis is a statistical process which enables prediction of relationships between variables. This book will give you a rundown explaining what regression analysis is, explaining you the process from scratch. Each chapter starts with explaining the theoretical concepts and once the reader gets comfortable with the theory, we move to the practical examples to support the understanding. By the end of this book you will know all the concepts and pain-points related to regression analysis, and you will be able to implement your learning in your projects.

Jan 2018 14h 4m

Regression Analysis with R

Regression Analysis with R

Regression analysis is a statistical process which enables prediction of relationships between variables. This book will give you a rundown explaining what regression analysis is, explaining you the process from scratch. Each chapter starts with explaining the theoretical concepts and once the reader gets comfortable with the theory, we move to the practical examples to support the understanding. By the end of this book you will know all the concepts and pain-points related to regression analysis, and you will be able to implement your learning in your projects.

Jan 2018 14h 4m

Hands-On Ensemble Learning with R

Hands-On Ensemble Learning with R

This book introduces you to the concept of ensemble learning and demonstrates how different machine learning algorithms can be combined to build efficient machine learning models. Use R to implement the popular trilogy of ensemble techniques, i.e. bagging, random forest and boosting, to build faster and more accurate machine learning models.

Jul 2018 12h 32m

Hands-On Data Science for Marketing

Hands-On Data Science for Marketing

This book will be an excellent resource for both Python and R developers and will help them apply data science and machine learning to marketing with real-world data sets. By the end of this book, you will be well equipped with the required knowledge and expertise to draw insights from data and improve your marketing strategies.

Mar 2019 15h 28m

Hands-On Data Science for Marketing

Hands-On Data Science for Marketing

This book will be an excellent resource for both Python and R developers and will help them apply data science and machine learning to marketing with real-world data sets. By the end of this book, you will be well equipped with the required knowledge and expertise to draw insights from data and improve your marketing strategies.

Mar 2019 15h 28m

Hands-On Data Science for Marketing

Hands-On Data Science for Marketing

This book will be an excellent resource for both Python and R developers and will help them apply data science and machine learning to marketing with real-world data sets. By the end of this book, you will be well equipped with the required knowledge and expertise to draw insights from data and improve your marketing strategies.

Mar 2019 15h 28m

Personalised recommendations for you

Based on your interests and search pattern

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m